Числа в python (faq)

Операторы Python

Оператор – это символ или функция, которая выполняет то или иное действие над данными. К примеру, символ + – это оператор сложения.

В Python присутствуют как общие, так и специальные математические операторы.

Ниже приведена таблица наиболее распространённых математических операторов Python.

Операция	Результат
x + y	Сложение (сумма x и y)
x – y	Вычитание (разница между x и y)
-x	Смена знака x
+x	Тождественность x
x * y	Умножение x на y
x / y	Деление x на y
x // y	Получение целой части от деления x на y
x % y	Остаток от деления x / y
x ** y	Возведение в степень

Также руководство охватывает использование операторов присваивания.

Логические операторы

Логические операторы – одни из самых важных, поскольку позволяют управлять потоком выполнения программы. В Python предусмотрено три оператора этого типа – and, or, not. Их легко запомнить, потому что они идентичны аналогичным словам на английском языке. Соответственно, они обозначают «и», «или», «не» соответственно. Рассмотрим эти операторы подробнее.

И (and). Оператор, выполняющий следующий алгоритм:

1. Сравнивает между собой два операнда.
2. Если оба выражения являются истинными, возвращается значение True. Если же хотя бы одно из них ложное, то возвращается False.

Приведем пример использования выражения.

>>> a = 7 > 7 and 2 > -1

>>> print(a)

Аналогично примерам, приведенным выше, здесь программа печатает результат выполнения своих операций по предыдущей строчке. Поскольку после обработки обнаружится результат «Ложь», то консоль также выдаст значение False.

Или (or). В этом случае истиной будет считаться тот результат, когда хотя бы одно из условий в операндах является истинным. Если же оба из них ложные, то выдается значение False.

>>> a = 7 > 7 or 2 > -1

>>> print(a)

Не (not). Этот оператор осуществляет инверсию значений. То есть, если на входе находится «Истина», то на выходе будет «Ложь». И наоборот. Так, в примере, который будет чуточку ниже, цифра 0 используется в качестве аргумента функции not. Соответственно, в консоли было выведено обратное значение – True (Ведь 0 – это «ложь» в классификации этого языка).

>>> a = not(0)

>>> print(a)

True

8 ответов

Лучший ответ

Делайте деление с плавающей точкой, затем конвертируйте в int. Никаких дополнительных модулей не требуется.

19

Tim
12 Ноя 2013 в 01:54

Вы также можете использовать десятичный модуль как часть стандартных библиотек python.

В частности, «оператор целочисленного деления // ведет себя аналогично, возвращая целочисленную часть истинного фактора (усеченную до нуля), а не его пол, чтобы сохранить обычную идентичность x == (x // y) * y + x % y: «

Также ознакомьтесь с , поскольку они есть несколько способов просмотра / округления вашей информации — потолок, вниз, пол, половина вниз, половина даже, половина вверх, вверх и 05 округления.

Десятичное число было написано как решение традиционной проблемы двоичной математики в мире, ожидающем десятичных решений

1

jjisnow
13 Авг 2017 в 21:57

По умолчанию деление целых чисел по Python возвращает слово (к отрицательной бесконечности) без возможности изменить это. Вы можете прочитать причину BDFL Почему.

Чтобы сделать округление вверх, вы должны использовать:

Чтобы выполнить усечение до нуля и сохранить целочисленное деление, используйте , если a или b отрицательны, и деление по умолчанию, если оба положительны.

Это будет делать целочисленное деление и всегда округлять до нуля:

Сноска

Интересно, что C99 заявляет, что по умолчанию используется округление до нуля:

Печать :

5

Community
23 Май 2017 в 12:00

Зачем изобретать велосипед, если есть отличная функция math.trunc ()?

jjisnow
15 Сен 2019 в 07:08

Что бы это ни стоило, мое любимое решение — это одно. Только целочисленная арифметика, одно деление и все остальное линейное время:

Это предполагает, что положителен, но в большинстве приложений, которые я видел, это правда. Если вам также нужно иметь дело с отрицательным , то функция становится немного более сложной:

Некоторые примеры выходов:

4

Mark Dickinson
19 Ноя 2013 в 18:42

Вбрасывая мою шляпу с несколькими альтернативными идеями:

Умножьте знак числа [abs (x) / x] на abs (x) / 2.

Выполните сложение, но если число меньше нуля, добавьте единицу, чтобы сместить его ближе к 0.

1

user764357user764357
12 Ноя 2013 в 03:48

Правильный код для этого, на мой взгляд, слишком неясен, чтобы писать как 1-строчный. Так что я бы поместил это в функцию, например:

Хорошие возможности: он работает для любого размера int, не вносит никаких корректировок в необработанный () результат, если в этом нет необходимости, только делает одно деление ( также делит под покрытиями), и не создает целых чисел больше, чем входные. Это может иметь или не иметь значения в вашей заявке; они становятся более важными (для скорости), если вы используете «большие» целые числа.

1

Tim Peters
12 Ноя 2013 в 02:37

Попробуй это. Работает только для чисел больше -1

1

Conor Patrick
12 Ноя 2013 в 01:55

Работа с комплексными числами

Для создания комплексного числа можно использовать функцию complex(a, b), в которую, в качестве первого аргумента, передается действительная часть, в качестве второго – мнимая. Либо записать число в виде  a + bj.

Рассмотрим несколько примеров.

Создание комплексного числа.

>>> z = 1 + 2j
>>> print(z)
(1+2j)
>>> x = complex(3, 2)
>>> print(x)
(3+2j)

Комплексные числа можно складывать, вычитать, умножать, делить и возводить в степень.

>>> x + z
(4+4j)
>>> x - z
(2+0j)
>>> x * z
(-1+8j)
>>> x  z
(1.4-0.8j)
>>> x ** z
(-1.1122722036363393-0.012635185355335208j)
>>> x ** 3
(-9+46j)

У комплексного числа можно извлечь действительную и мнимую части.

>>> x = 3 + 2j
>>> x.real
3.
>>> x.imag
2.

Для получения комплексносопряженного число необходимо использовать метод conjugate().

>>> x.conjugate()
(3-2j)

Печать чисел в Style

Для отображения чисел пользователю необходимо вставить числа в строку. Вы можете сделать это с помощью f-строк, заключив переменную, присвоенную номеру, фигурными скобками:

Эти фигурные скобки поддерживают простой язык форматирования, который можно использовать для изменения внешнего вида значения в окончательной отформатированной строке.

Например, чтобы отформатировать значение n в приведенном выше примере до двух десятичных знаков, замените содержимое фигурных скобок в строке f с :

Двоеточие () после переменной означает, что все, что находится после нее, является частью спецификации форматирования. В этом примере спецификация форматирования – .

в округляет число до двух десятичных знаков, а указывает Python отображать как число с фиксированной точкой. Это означает, что число отображается ровно с двумя десятичными знаками, даже если исходное число имеет меньше десятичных знаков.

Когда , результат равен . Как и , Python округляет связи даже при форматировании чисел внутри строк. Итак, если вы замените на , то результат будет :

Чтобы округлить до одного десятичного знака, замените на :

Когда вы форматируете число как фиксированную точку, оно всегда отображается с указанным вами точным количеством десятичных знаков:

Вы можете вставить запятые, чтобы сгруппировать целую часть больших чисел тысячами с помощью параметра :

Чтобы округлить до некоторого числа десятичных знаков, а также сгруппировать по тысячам, поставьте перед в вашей спецификации форматирования:

Спецификатор полезен для отображения значений валюты:

Еще одна полезная опция – , которая используется для отображения процентов. Параметр умножает число на 100 и отображает его в формате с фиксированной точкой, за которым следует знак процента.

Параметр всегда должен стоять в конце спецификации форматирования, и его нельзя смешивать с параметром . Например, отображает число в процентах с точностью до одного десятичного знака:

Мини-язык форматирования является мощным и обширным. Вы видели здесь только основы. Для получения дополнительной информации ознакомьтесь с .

Комплексные числа[править]

Пусть x2 = 2. Большинство из нас будут способны найти первый корень x=2{\displaystyle x={\sqrt {2}}}. Более продвинутые в математике заметят, что имеется и второй корень x=−2{\displaystyle x=-{\sqrt {2}}}. Но встретившись с выражением x2 = -2 решение смогут найти лишь немногие люди, знакомые с комплексными числами. Если вы только собираетесь стать ученым, настоятельно советуем познакомиться сейчас с этими замечательными числами перед тем, как изучить дальнейшие примеры, на которых вы сможете проверить свои новые знания.

Комплексная арифметика в Pythonправить

Python поддерживает расчеты с комплексными числами. Мнимая часть записывается через j, вместо i в математике. Комплексное число 2-3i соответственно будет записано как 2-3j. Ниже показан простой сеанс работы с комплексными числами и примеры простой комплексной арифметики:

>>> u = 2.5 + 3j       # создаем комплексное
>>> v = 2              # а это целое
>>> w = u + v          # комплексное + целое
>>> w
(4.5+3j)

>>> a = -2
>>> b = 0.5
>>> s = a + b*1j       # complex из двух float
>>> s = complex(a, b)  # другой способ
>>> s
(-2+0.5j)
>>> s*w                # complex*complex
(-10.5-3.75j)
>>> sw                # complex/complex
(-0.25641025641025639+ 0.28205128205128205j)

Кроме того объект типа complex легко может быть разложен на реальную и мнимую части и для него может быть найдено сопряженное (conjugate) число:

>>> s.real
-2.0
>>> s.imag
0.5
>>> s.conjugate()
(-2-0.5j)

Комплексные функции Pythonправить

Для работы с функциями комплексных переменных следует использовать специальную библиотеку — cmath:

>>> from cmath import sin, sinh
>>> r1 = sin(8j)
>>> r1
1490.4788257895502j
>>> r2 = 1j*sinh(8)
>>> r2
1490.4788257895502j

Комплексные числа

В языке программирования Python также поддерживается работа с комплексными числами. Подобная информация представлена в виде пары значений: действительной и мнимой части, которые разделяются символом операции сложения. Также в завершении мнимой составной части комплексного числа обязательно должна стоять буква j. В следующем фрагменте кода демонстрируется создание комплексной переменной c и выводится вся информация о ней:

c = 1 + 2j # комплексное число
print("c = " + str(c))
print(type(c))

c = (1+2j)
<type 'complex'>

Можно получить действительную и мнимую часть чисел отдельно. Для этого следует использовать real и image:

c = (1+2j)
print(c.real)
print(c.imag)

1.0
2.0

Сумма в питоне и разность в питоне

В Python операторы суммы и разности выполняют те же операции, что и в математике. Поэтому вы можете использовать этот язык программирования как калькулятор.

Рассмотрим некоторые примеры. Начнём с целых чисел:

print(1 + 5)

Вывод

6

Вместо передачи целых чисел напрямую в функцию  мы можем инициализировать переменные для этих значений:

a = 88
b = 103
print(a + b)

Вывод

191

Целые числа могут быть как положительными, так и отрицательными. Поэтому можно добавлять отрицательные числа к положительным:

c = -36
d = 25
print(c + d)

Вывод

-11

Прибавление работает аналогично и с числами с плавающей запятой:

e = 5.5
f = 2.5
print(e + f)

Вывод

8.0

Синтаксис разности тот же, что и для прибавления, за исключением того, что вместо оператора сложения () необходимо использовать оператор вычитания ():

g = 75.67
h = 32
print(g - h)

Вывод

43.67

В этом примере мы вычитаем целое число из числа с плавающей точкой. Python возвратит число с плавающей точкой, если хотя бы одно из чисел выражения является числом с плавающей точкой.

Идентификационные операторы

Python provides two operators, and , that determine whether the given operands have the same identity—that is, refer to the same object. This is not the same thing as equality, which means the two operands refer to objects that contain the same data but are not necessarily the same object.
Here is an example of two object that are equal but not identical:

>>> x = 1001
>>> y = 1000 + 1
>>> print(x, y)
1001 1001
>>> x == y
True
>>> x is y
False

Here, and both refer to objects whose value is . They are equal. But they do not reference the same object, as you can verify:

>>> id(x)
60307920
>>> id(y)
60307936

and do not have the same identity, and returns .
You saw previously that when you make an assignment like , Python merely creates a second reference to the same object, and that you could confirm that fact with the function. You can also confirm it using the operator:

>>> a = 'I am a string'
>>> b = a
>>> id(a)
55993992
>>> id(b)
55993992
>>> a is b
True
>>> a == b
True

In this case, since and reference the same object, it stands to reason that and would be equal as well.
Unsurprisingly, the opposite of is :

>>> x = 10
>>> y = 20
>>> x is not y
True

LDA для более чем одного предсказателя

Расширяя теперь для нескольких предикторов, мы должны предположить, чтоИксвзят измногомерное распределение Гаусса, с классом среднего вектора и общей ковариационной матрицей.

Пример коррелированного и некоррелированного гауссовского распределения показан ниже.

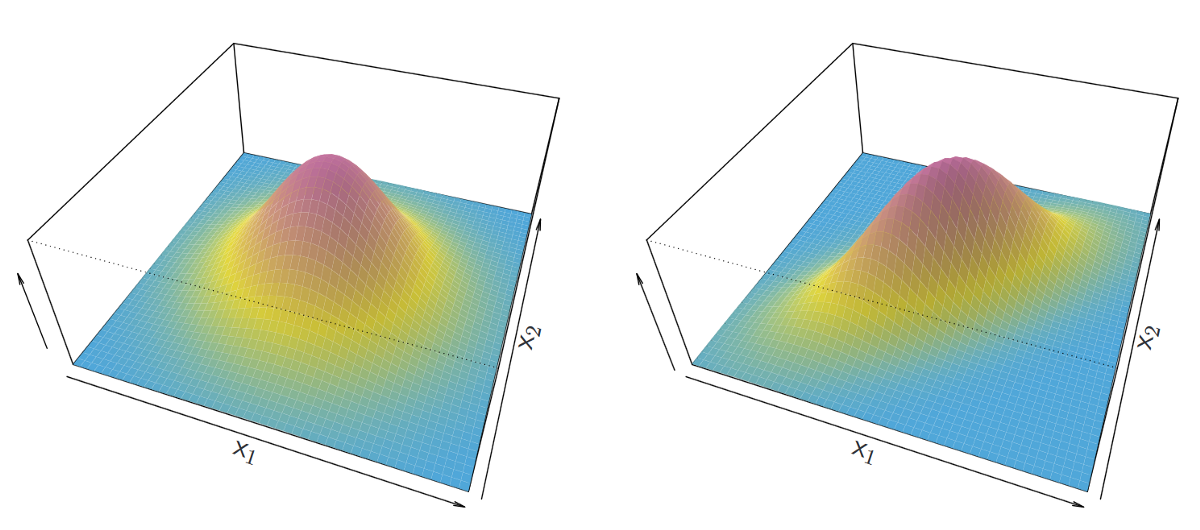
Слева: некоррелированное нормальное распределение. Справа: коррелированное нормальное распределение

Теперь, выражая дискриминантное уравнение с помощью векторной записи, получим:

Дискриминантное уравнение с матричной нотацией

Как видите, уравнение остается прежним. Только на этот раз мы используем векторную нотацию для размещения многих предикторов.

Создание класса в Python:

 Определение класса начинается с ключевого слова class, после него следует имя класса и двоеточие.

class имя_класса:           # тело класса           # объявление конструктора          # объявление атрибутов          # объявление методов 

Основные определения 

Метод __init__  или Конструктор

 В процессе создания объекта  атрибутам класса необходимо задать начальные значения

Это действие  называется инициализацией.  Для этой цели используется   специальный метод __init__(), который  называется методом инициализации или  конструктором.    Метод __init__ запускается при создании экземпляра класса — один раз. Обратите внимание на двойные подчёркивания в начале и в конце имени. Синтаксис метода следующий:

def __init__(self, параметр1, параметр2):self.атрибут1 = параметр1             self.атрибут2 = параметр2

Два символа подчеркивания в начале  __init__ и  два символа подчеркивания в конце обязательны. Параметров у конструктора  параметр1, параметр2 может быть сколько угодно, но первым дожен быть параметр  self.

Умножение и деление

Операции умножения и деления, как сложение и вычитание, выполняются в Python так же, как в обычной математике. Для умножения Python использует *, для деления – /.

Например:

При делении в Python 3 частное всегда возвращается в виде числа с плавающей точкой, даже если вы делите целые числа:

Это одно из главных различий между Python 2 и Python 3. Python 3 возвращает дробный результат, потому при делении 11 на 2 вы получите 5.5. В Python 2 деление привязано к типам данных, потому при делении целого числа невозможно получить число с плавающей точкой; поэтому при делении 11 на 2 Python 2 возвращает 5.

Когда числа по обе стороны символа деления являются целыми, выполняется деление floor, то есть, для фактора х Python 2 возвращает наибольшее целое число меньше или равное х. К примеру, при делении 5 / 2 таким числом будет 2.

Чтобы выполнить деление floor и получить только целую часть числа, Python 3 использует оператор //. К примеру, разделив 100//40, вы получите 2.

Операции с системами счисления

Как гласит математика и информатика, числа можно представить как в десятичной, так и в двоичной системе счисления. Допустим, число 19 в двоичной системе имеет вид 10011. Также можно переводить числа из одной системы в другую. В Python для этого есть ряд функций:
• int(, ) — функция нужна для преобразования к целому числу. По умолчанию речь идёт о десятичной системе, однако можно задать любое основание в пределах чисел 2-36.
• bin(x) — функция для преобразования целого числа в двоичную строку;
• hex(х) — аналогично, но действительное целое число преобразуется в шестнадцатеричную строку;
• oct(х) — для преобразования чисел в восьмеричную строку.

Пример:

>>>
>>> a = int('19') # Строка переводится в число
>>> b = int('19.5')  # Строка не является числом
Traceback (most recent call last):
  File "", line 1, in
ValueError invalid literal for int() with base 10 '19.5'
>>> c = int(19.5)  # Отсекает дробную часть, если применена к числу с плавающей точкой
>>> print(a, c)
19 19
>>> bin(19)
'0b10011'
>>> oct(19)
'0o23'
>>> hex(19)
'0x13'
>>> 0b10011  # Вариант записи числовых констант
19
>>> int('10011', 2)
19
>>> int('0b10011', 2)
19

Таблица «Функции и методы строк»

Функция или метод	Назначение
S = ‘str’; S = «str»; S = »’str»’; S = «»»str»»»	Литералы строк
S = «s\np\ta\nbbb»	Экранированные последовательности
S = r»C:\temp\new»	Неформатированные строки (подавляют экранирование)
S = b»byte»	Строка байтов
S1 + S2	Конкатенация (сложение строк)
S1 * 3	Повторение строки
S	Обращение по индексу
S	Извлечение среза
len(S)	Длина строки
S.find(str, ,)	Поиск подстроки в строке. Возвращает номер первого вхождения или -1
S.rfind(str, ,)	Поиск подстроки в строке. Возвращает номер последнего вхождения или -1
S.index(str, ,)	Поиск подстроки в строке. Возвращает номер первого вхождения или вызывает ValueError
S.rindex(str, ,)	Поиск подстроки в строке. Возвращает номер последнего вхождения или вызывает ValueError
S.replace(шаблон, замена)	Замена шаблона на замену. maxcount ограничивает количество замен
S.split(символ)	Разбиение строки по разделителю
S.isdigit()	Состоит ли строка из цифр
S.isalpha()	Состоит ли строка из букв
S.isalnum()	Состоит ли строка из цифр или букв
S.islower()	Состоит ли строка из символов в нижнем регистре
S.isupper()	Состоит ли строка из символов в верхнем регистре
S.isspace()	Состоит ли строка из неотображаемых символов (пробел, символ перевода страницы (‘\f’), «новая строка» (‘\n’), «перевод каретки» (‘\r’), «горизонтальная табуляция» (‘\t’) и «вертикальная табуляция» (‘\v’))
S.istitle()	Начинаются ли слова в строке с заглавной буквы
S.upper()	Преобразование строки к верхнему регистру
S.lower()	Преобразование строки к нижнему регистру
S.startswith(str)	Начинается ли строка S с шаблона str
S.endswith(str)	Заканчивается ли строка S шаблоном str
S.join(список)	Сборка строки из списка с разделителем S
ord(символ)	Символ в его код ASCII
chr(число)	Код ASCII в символ
S.capitalize()	Переводит первый символ строки в верхний регистр, а все остальные в нижний
S.center(width, )	Возвращает отцентрованную строку, по краям которой стоит символ fill (пробел по умолчанию)
S.count(str, ,)	Возвращает количество непересекающихся вхождений подстроки в диапазоне (0 и длина строки по умолчанию)
S.expandtabs()	Возвращает копию строки, в которой все символы табуляции заменяются одним или несколькими пробелами, в зависимости от текущего столбца. Если TabSize не указан, размер табуляции полагается равным 8 пробелам
S.lstrip()	Удаление пробельных символов в начале строки
S.rstrip()	Удаление пробельных символов в конце строки
S.strip()	Удаление пробельных символов в начале и в конце строки
S.partition(шаблон)	Возвращает кортеж, содержащий часть перед первым шаблоном, сам шаблон, и часть после шаблона. Если шаблон не найден, возвращается кортеж, содержащий саму строку, а затем две пустых строки
S.rpartition(sep)	Возвращает кортеж, содержащий часть перед последним шаблоном, сам шаблон, и часть после шаблона. Если шаблон не найден, возвращается кортеж, содержащий две пустых строки, а затем саму строку
S.swapcase()	Переводит символы нижнего регистра в верхний, а верхнего – в нижний
S.title()	Первую букву каждого слова переводит в верхний регистр, а все остальные в нижний
S.zfill(width)	Делает длину строки не меньшей width, по необходимости заполняя первые символы нулями
S.ljust(width, fillchar=» «)	Делает длину строки не меньшей width, по необходимости заполняя последние символы символом fillchar
S.rjust(width, fillchar=» «)	Делает длину строки не меньшей width, по необходимости заполняя первые символы символом fillchar
S.format(*args, **kwargs)	Форматирование строки

Приведение типов

Используя стандартные средства языка Python, можно достаточно легко менять типовую принадлежность практически любой переменной. Для этого существуют методы, такие как int, float, complex, bin, oct, hex. Три последние функции позволяют перевести число либо переменную в десятичную, восьмеричную и шестнадцатеричную систему соответственно. Следующий фрагмент кода демонстрирует работу всех шести вышеописанных методов:

i = int(67.23) # вещественное число усекается до целого
f = float('1304') # строка становится вещественным числом
c = complex(2, 6) # формируется комплексное число
b = bin(42) # перевод числа в двоичную систему
o = oct(993) # перевод числа в восьмеричную систему
x = hex(4152) # перевод числа в шестнадцатеричную систему
print("i = " + str(i))
print("f = " + str(f))
print("c = " + str(c))
print("b = " + str(b))
print("o = " + str(o))
print("x = " + str(x))

i = 67
f = 1304.0
c = (2+6j)
b = 0b101010
o = 01741
x = 0x1038

Операторы сравнения

Оператор
Пример
Смысл
Результат

Эквивалентно

если значение равно значению , в противном случае

Не эквивалентно

если не равно и в противном случае

Меньше

если меньше чем , в противном случае

Меньше или равно

если меньше или равно , в противном случае

Больше

если больше , в противном случае

Больше или равно

если больше или равно , в противном случае

Вот примеры используемых операторов сравнения:

>>> a = 10
>>> b = 20
>>> a == b
False
>>> a != b
True
>>> a <= b
True
>>> a >= b
False
>>> a = 30
>>> b = 30
>>> a == b
True
>>> a <= b
True
>>> a >= b
True

Операторы сравнения обычно используются в булевых контекстах, таких как условные операторы и операторы цикла, для процессом вычислений, как вы увидите позже.

Равенство для значений с плавающей точкой

Вспомните из более раннего обсуждения , что значение хранится внутри для объекта может быть не совсем таким, как вы думаете. По этой причине не рекомендуется сравнивать значения с плавающей точкой для точного равенства. Рассмотрим этот пример:

>>> x = 1.1 + 2.2
>>> x == 3.3
False

Бабах! Внутренние представления операндов сложения не совсем равны и , поэтому вы не можете полагаться на для точного сравнения с .

Предпочтительным способом определения того, являются ли два значения с плавающей точкой «равными», является вычисление того, находятся ли они близко друг к другу, с учетом некоторого допуска. Посмотрите на этот пример:

>>> tolerance = 0.00001
>>> x = 1.1 + 2.2
>>> abs(x - 3.3) < tolerance
True

Функция возвращает абсолютное значение. Если абсолютное значение разности между двумя числами меньше указанного допуска, они достаточно близки друг к другу, чтобы считаться равными.

Типы чисел в Python.

В Python числа делятся на несколько категорий в соответствии со способом их использования. Основные это целые числа (int) и вещественные (float) или числа с плавающей точкой. Чтобы узнать к какому типу относится число или переменная, можно воспользоваться встроенной функцией type(). Запустите командную строку и активируйте Python. В скобках введите число или переменную, чтобы узнать ее тип.

>>> type(5)                                                                  <class ‘int’>

>>> type(12.5)<class ‘float’>

>>> x = 10
>>> type(x)<class ‘int’>

Значение 12,5 является числом с плавающей точкой, поэтому Python выводит строку float. Переменная x содержит целое число 10, поэтому Python выводит тип int (сокращение от integer). 

Проверьте свое понимание

Отобразите валюту

Выведите число 150000 в виде валюты с тысячами, сгруппированными через запятую. Валюта должна отображаться с двумя десятичными знаками и начинаться с символа доллара США.

Решение

Давайте постепенно наращивать нашу f-строку.

Во-первых, f-строка, которая отображает значение 150000 без какого-либо форматирования, выглядит так:

Это может показаться странным, но заставляет вас добавить спецификаторы форматирования.

Чтобы значение отображалось как число с плавающей запятой, поставьте двоеточие () после числа 150000, а затем букву :

По умолчанию Python отображает число с точностью до шести десятичных знаков. Валюта должна иметь только два десятичных знака точности, поэтому вы можете добавить между и :

Чтобы отобразить номер с цифрами, сгруппированными через запятую, вставьте запятую () между двоеточием () и точкой ():

Наконец, добавьте знак доллара () в начало строки, чтобы указать, что значение указано в долларах США:

F-строки – это всего лишь один из способов форматирования чисел для отображения.

Когда будете готовы, можете переходить к следующему разделу.

Поезд / тестовый сплит

Прежде чем углубляться в моделирование и делать прогнозы, нам нужно разделить наш набор данных на обучающий набор и набор тестов. Таким образом, мы можем обучить алгоритм на тренировочном наборе и делать прогнозы на тестовом наборе. Метрики ошибок будут намного более релевантными, так как алгоритм будет делать прогнозы для данных, которых он не видел раньше.

Мы можем легко разделить набор данных следующим образом:

Вот,Yпросто цель (ядовитая или съедобная). Затем,Иксэто просто все особенности набора данных. Наконец, мы используемtrain_test_splitфункция.test_sizeПараметр соответствует части набора данных, которая будет использоваться для тестирования. Обычно мы используем 20%. Затемrandom_stateПараметр используется для воспроизводимости. Он может быть установлен на любое число, но он гарантирует, что при каждом запуске кода набор данных будет разделен одинаково. Если нетrandom_stateпри условии, что поезд и набор тестов будут различаться, так как функция разбивает их случайным образом.

Хорошо, мы официально готовы начать моделирование и делать прогнозы!

Битовые операторы

На практике, используются довольно редко. Но применяются. И знать их тоже надо. 

Для начала надо раскрыть, что такое побитовые операции в целом. Они выполняются над разрядами числа по специальным формулам, каждая из которых зависит от операторов.

Поэтому важно рассмотреть их более подробно. Бинарное И (&)

Полный аналог оператора and, только который работает с битами. Точно так же, как и любой другой битовый оператор, он выполняет операции с каждой парой битов по отдельности, осуществляя с ними действия в соответствии с этой таблицей

Бинарное И (&). Полный аналог оператора and, только который работает с битами. Точно так же, как и любой другой битовый оператор, он выполняет операции с каждой парой битов по отдельности, осуществляя с ними действия в соответствии с этой таблицей.

0 & 0 = 0

0 & 1 = 0

1 & 0 = 0

1 & 1 = 1

То есть, если первый бит в первой последовательности будет 0 и во второй последовательности битов первый бит будет 0, то после выполнения этой операции получится значение 0. 

Точно так же и с каждым последующим битом. Предположим, у нас есть две последовательности:

00100101

00111010

После того, как каждая из этих последовательностей битов будет обработана оператором, получится следующая последовательность:

00100000

Естественно, передавать значения можно и в десятичной форме. В таком случае они будут преобразованы в двоичную и выполнены соответствующие вычисления. А потом они снова будут преобразованы в десятичную систему. 

Например, если выполнить побитовое «И» с числами 2 и 3, то получится две последовательности битов в двоичной форме:

10

11

Если сопоставить с таблицей выше, то после побитового И будет выдан следующий результат:

10.

То есть, на вывод уйдет цифра 2, поскольку после выполнения операции побитового И 1 и 1 дали 1, а 0 и 1 дали 0. В результате, получилось значение 10, что соответствует 2.

По аналогичному принципу работают и другие бинарные операторы.

Бинарное ИЛИ (|). Соответствует побитовой операции or. 

Общая таблица сопоставления битов с использованием этого оператора следующая.

0 | 0 = 0

0 | 1 = 1

1 | 0 = 1

1 | 1 = 1

То есть, если ввести такую строку кода, получится на выходе 3.

>>> 2|3

Почему? Потому что эти две десятичные цифры переводятся в следующие две последовательности.

10

11

1 на 1 дает 1, и 0 на 1 дает 1. Соответственно, получилось число 11 в двоичной форме, что соответствует 3 в десятичной. Поэтому такой вывод.

Бинарное ИЛИ НЕТ (^). С помощью этой функции выполняется исключающее между двумя операндами, переведенными в двоичную форму. Сопоставление осуществляется по таким правилам.

0 ^ 0 = 0

0 ^ 1 = 1

1 ^ 0 = 1

1 ^ 1 = 0

Таким образом, если выполнить соответствующую операцию с теми же самыми числами, то получится в результате 1. Ведь цифра 2 у нас 10, а 11 – это 3. Таким образом, если сопоставить разряды по правилам, получится в итоге 01.

>>> 2^3

10

11

––

01

Инвертирующий оператор. С его помощью пользователь может инвертировать 0 в 1 и наоборот.

Например, если применить его к 2, то получится в результате -3. Почему? Потому что в двоичном формате цифра 2 – это 00000010. Если же ее инвертировать, то получится 11111101, что соответствует двоичной -3. Таким образом, получится в итоге обычная 2. 

Естественно, работает все и абсолютно наоборот. Ведь если 11111101 заменить на противоположные значения, то получится на выходе та же цифра 3.

Бинарный сдвиг влево и вправо. Осуществляет сдвиг левого оператора на ту позицию, которая есть справа. Например, если попробовать сдвинуть вправо бинарную 3 (то есть, 11) на два положения влево, то в результате получится число 00, поскольку единицы ушли за пределы разряда.

И такой принцип дальше. То есть, первый операнд – это то число, сдвиг которого надо осуществить. Второй же операнд – количество бит, на которое необходимо его выполнить.

Пример.

>>> 3>>2

>>> 3>>1

Операторы присваивания

Теперь перейдем к рассмотрению операторов присваивания. Они предназначены для того, чтобы передавать переменной определенные значения как принадлежащие другим переменным, так и появившиеся вследствие их обработки. Операторы присваивания нужны еще и для того, чтобы назначать переменным объекты, с которыми можно дальше выполнять определенные действия. 

Таким образом, спектр применений операторов этого типа довольно обширный.

Присваивание. Выглядит, как математический знак «равно». Это классический оператор, типичный пример применения которого – присваивание значения переменной. Давайте приведем такой пример. 

>>> a = 7

>>> print(a)

7

Сложение и присваивание. Этот оператор не просто присваивает правую часть левой, но и увеличивает её на определённое значение. 

Выглядит он, как знак плюса и равно вместе (+=). 

Чтобы было более понятно, давайте рассмотрим этот код. 

>>> a += 2

>>> print(a)

После выполнения соответствующих арифметических действий интерпретатор выдаст значение 9 при условии, что значение переменной a было 7. 

То есть, этот оператор идентичен выражению a = a + 2.

Вычитание и присваивание. Противоположный предыдущему оператор. Если мы используем выражение a -= 2, это будет значить то же самое, что и выражение a = a – 2.

Деление и присваивание. Выполняет операцию деления между двумя операндами. После этого получившееся значение присваивается соответствующей переменной. Позволяет два действия: деление и присваивание запрограммировать всего одной строчкой кода. Можно также использовать переменные, объекты и другие значения, которые можно присвоить левой части, в правой. 

Приведем пример.

>>> a /= 7

>>> print(a)

Умножение и присваивание. Выполняет аналогичную последовательность действий для двух операндов. Сначала выполняется арифметическая операция с двумя операндами, а потом получившееся значение присваивается левому. В данном случае такой арифметической операцией служит умножение. 

>>> a *= 8

>>> print(a)

Деление по модулю и присваивание. Этот оператор выполняет сразу три действия:

1. Делит первый операнд на второй. 
2. Определяет целое число.
3. Присваивает это целое число той переменной, которая находится в правом операнде. 

Синтаксис элементарный:

>>> a %= 3

>>> print(a)

Эта программа выполняет три описанных выше действия, после чего получившийся результат печатает в консоли или нижней строке онлайн-интерпретатора. Например, если переменная a = 10, то будет выведено число 3.

Возведение в степень и присваивание. Этот оператор выполняет два действия:

1. Берет левый операнд и возводит его в степень, равная числу справа.
2. Получившееся число сразу становится значением переменной слева. 

Здесь, как и в других операторах, можно использовать переменные в качестве правого операнда. Например, если в левой части находится переменная с числом 4, а в правой – число 2, то на вывод будет отправлено число 16.

>>> a **= 2

>>> print(a)

16

Деление с остатком и присваивание. В принципе, вы уже поняли, как работает и записывается выражение с этим оператором. Он может получать остаток от деления первого числа на второе и возвращать его в ту переменную, которая стоит справа. Например, эта программа выводит остаток от деления на экран.

>>> a //= 3

>>> print(a)