Как в ворде поставить знак умножения

Как поставить точку над буквой в Word

Кодовый набор символов Unicode определяет серию кодов, которые позволяют комбинировать диакритические знаки, например, ввести букву и затем поставить точку над буквой. Код для размещения точки над буквой — «0307.» Чтобы поставить точку над буквой в Word, введите букву, введите «0307» и нажмите «Alt-X», чтобы вызвать диакритическую комбинацию.

Над некоторыми буквами польского алфавита есть точка.

Кредит изображения: Comstock Images / Stockbyte / Getty Images

Многие популярные шрифты, такие как Arial, Times New Roman и Calibri, содержат буквы с точками над ними в качестве стандартных символов шрифта.Чтобы вставить один из этих символов шрифта в Word, выберите «Вставить» в меню, «Символ» на панели ленты и выберите «Дополнительные символы . ». Выберите шрифт в поле выбора шрифта, найдите символ, который вы хотите вставить. , щелкните, чтобы выделить его, и выберите «Вставить».

Вставка знака умножения в Microsoft Word

Когда нужно поставить знак умножения в MS Word, большинство пользователей выбирают не самое правильное решение. Кто-то ставит “*”, а кто-то поступает еще более радикально, ставя обычную букву “x”. Оба варианта в корне неправильны, хоть и могут “прокатить” в некоторых ситуациях. Если же вы печатаете в Ворде примеры, уравнения, математические формулы, обязательно нужно ставить правильный знак умножения.

Урок: Как в Word вставить формулу и уравнение

Наверное, многие еще со школы помнят, что в различной литературе можно столкнуться с различными обозначениями знака умножения. Это может быть точка, а может быть так называемая буква “x”, с разницей лишь в том, что оба эти символа должны находиться посреди строки и уж точно быть меньше основного регистра. В этой статье мы расскажем о том, как поставить в Ворде знак умножить, каждое из его обозначений.

Урок: Как в Word поставить знак степени

Добавление знака умножения в виде точки

Вы, наверное, знаете о том, что в Ворде имеется довольно большой набор неклавиатурных знаков и символов, которые во многих случаях могут оказаться очень полезными. Мы уже писали об особенностях работы с этим разделом программы, и знак умножения в виде точки мы тоже будем искать там.

Урок: Добавление символов и специальных знаков в Word

Вставка знака через меню “Символ”

1. Кликните в том месте документа, где нужно поставить знак умножения в виде точки, и перейдите во вкладку “Вставка”.

Примечание: Между цифрой (числом) и знаком умножения должен стоять пробел, также пробел должен стоять и после знака, перед следующий цифрой (числом). Как вариант, можно сразу написать те числа, которые нужно перемножить, и сразу поставить между ними два пробела. Знак умножения будем добавлять непосредственно между этими пробелами.

2. Откройте диалоговое окно “Символ”. Для этого в группе “Символы” нажмите кнопку “Символ”, а затем выберите пункт “Другие символы”.

3. В выпадающем меню “Набор” выберите пункт “Математические операторы”.

Урок: Как в Ворде поставить знак суммы

4. В изменившемся списке символов найдите знак умножения в виде точки, кликните по нему и нажмите “Вставить”. Закройте окно.

5. Знак умножения в виде точки будет добавлен в указанном вами месте.

Вставка знака с помощью кода

У каждого знака, представленного в окне “Символ”, есть свой код. Собственно, именно в этом диалоговом окне и можно подсмотреть, какой код имеет знак умножения в виде точки. Там же вы сможете увидеть комбинацию клавиш, которая поможет преобразовать введенный код в знак.

Урок: Горячие клавиши в Word

1. Установите указатель курсора в том месте, где должен находиться знак умножения в виде точки.

2. Введите код “2219” без кавычек. Делать это нужно на цифровом блоке клавиатуры (расположен справа), предварительно убедившись в том, что режим NumLock активен.

3. Нажмите “ALT+X”.

4. Введенные вами цифры будут заменены на знак умножения в виде точки.

Добавление знака умножения в виде буквы “x”

Ситуация с добавлением знака умножения, представленного в виде некоего крестика или, что более близко, уменьшенной буквы “x”, несколько сложнее. В окне “Символ” в наборе “Математические операторы”, как и в других наборах, вы его не найдете. И все же, добавить этот знак можно с помощью специального кода и еще одной клавиши.

Урок: Как в Ворде поставить знак диаметра

1. Установите курсор в том месте, где должен находиться знак умножения в виде крестика. Переключитесь в английскую раскладку.

2. Зажмите клавишу “ALT” и введите на цифровом блоке клавиатуры (справа) код “0215” без кавычек.

Примечание: Пока вы держите клавишу “ALT” и вводите цифры, они не отображаются в строке — так и должно быть.

3. Отпустите клавишу “ALT”, на этом месте появится знак умножения в виде буквы “x”, расположенный посреди строчки, как мы с вами привыкли это видеть в книгах.

Вот, собственно, и все, из этой небольшой статьи вы узнали, как в Word поставить знак умножения, будь то точка или диагональный крестик (буква “x”). Осваивайте новые возможности Ворд и используйте в полной мере потенциал этой программы. Мы рады, что смогли помочь Вам в решении проблемы. Опишите, что у вас не получилось.Наши специалисты постараются ответить максимально быстро.

Использование[править | править код]

Символ ×{\displaystyle \times }править | править код

Кроме умножения чисел, символ ×{\displaystyle \times } используется во многих других ситуациях. Примеры.

• Векторное произведение двух векторов: a→×b→.{\displaystyle {\vec {a}}\times {\vec {b}}.}
• Декартово произведение двух множеств: A×B.{\displaystyle A\times B.}
• Число строк и столбцов в матрице: n×n.{\displaystyle n\times n.}
• Геометрический размер (габариты) объекта — например, комната 8×5{\displaystyle 8\times 5} метров.
• Используется в языке программирования APL как унарный оператор для обозначения функции знака (sgn).
• Статистическое взаимодействие между двумя независимыми переменными.
• Код увеличения, например: 10×{\displaystyle 10\times } означает десятикратное увеличение.
• В таксономии знак умножения используется в качестве знака гибридного происхождения.

Для ввода с клавиатуры символа ×{\displaystyle \times } в среде Microsoft Windows следует, прижав клавишу Alt, набрать на цифровой клавиатуре сочетаниеAlt+215.

Символ интерпунктаправить | править код

Центрированная точка используется в некоторых древних и современных языках для словоразделения, указания особенностей произношения и т. д.. В математике она может обозначать скалярное произведение векторов, произведение матриц и других математических объектов.

Для ввода с клавиатуры символа интерпункта в среде Microsoft Windows следует, прижав клавишу Alt, набрать на цифровой клавиатуре сочетание Alt+25 (для жирной точки — Alt+149).

Какие часто используемые знаки есть на клавиатуре

Если внимательно посмотреть на клавиатуру, то можно увидеть, что многие знаки скрываются в цифровом ряду и с правой стороны буквенных рядов, последние клавиши. Для ввода при печати знаков вместо букв или цифр нужно переключить верхний регистр клавишей Shift.

Если идти по порядку, начиная с цифры 1, то таким способом при печати русских текстов вводится:

1) восклицательный знак «!»;2) открывающиеся и закрывающиеся кавычки в начале и конце фразы «…»;3) затем при необходимости знак номера «№»;4) точка с запятой «;»;5) «%»;6) двоеточие «:»;7) вопросительный знак «?»;8) знак звездочка «*», который используется и как знак умножения при компьютерных вычислениях;9) круглая открывающаяся «(»;10) круглая закрывающаяся скобка «)» на клавише с цифрой 0;11) дефис и знак «-» – в компьютерном варианте выглядят одинаково. Знак тире (более длинный) появляется автоматически с использование пробелов до и после этого знака в текстовых программах или же вводится с помощью специального кода.12) знак равно «=» и знак «+» в верхнем регистре, т.е. в комбинации с клавишей Shift.

Примечательно, что восклицательный знак, %, *, круглые скобки находятся как в русской, так и в английской раскладке клавиатуры на одних и тех же клавишах.

Но некоторые знаки существуют только в английской раскладке. Например, квадратные и фигурные {…} скобки, которые находятся на клавишах с русскими буквами Х (открывающиеся) и Ъ (закрывающиеся), «>» (клавиша с русской буквой Ю) и меньше «Редко используемые знаки на клавиатуре

В повседневной жизни обычному пользователю редко приходится пользоваться знаками, существующими только в английской раскладке: разные варианты кавычек “…”, ‘…’, `…`, черточек «|», прямой «/» и обратный «\» слеш, тильда «~». А вот знак параграфа «§» или градуса «°» не помешал бы , но на клавиатуре их нет. Приходится вводить в текст некоторые символы другим способом.

Большинство пользователей персонального компьютера, которые не очень хорошо владеют программой Word, ставят вместо подлинного знака умножения символ *, а то и вовсе букву х. Конечно же, это абсолютно неправильно. В данной статье дана информация о том, как в «Ворде» поставить знак умножения точкой или крестиком. Именно эти символы являются верными с математической точки зрения.

Основные возможности редактора формул

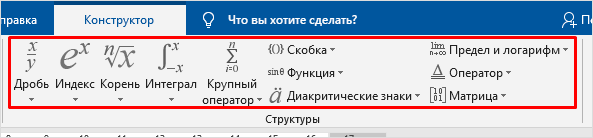
Мы рассмотрели с вами самые простые примеры использования редактора уравнений. Давайте теперь подробнее остановимся на доступных опциях. Добавляем новую формулу и смотрим на меню вкладки “Конструктор”.

Слева есть вкладка “Уравнение”, в ней собраны стандартные математические выражения и дополнительные материалы с сайта office.com. Просмотрите их, возможно, какие-то шаблоны вам пригодятся, и не надо будет набирать их вручную.

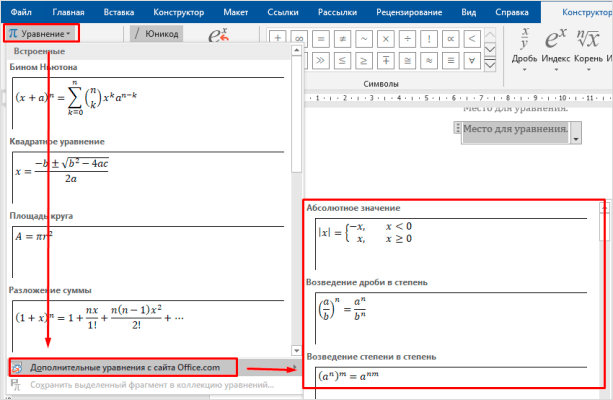
В том же левом углу есть опция, которая позволяет написать выражение вручную, как в тетради, а редактор сделает из нашей “писанины” печатные символы. Классная функция, но пока не до конца доработана, так что будьте внимательны. Если требуется строгое оформление документа, лучше все-таки набрать уравнение с использованием встроенных операторов или подправить его при необходимости.

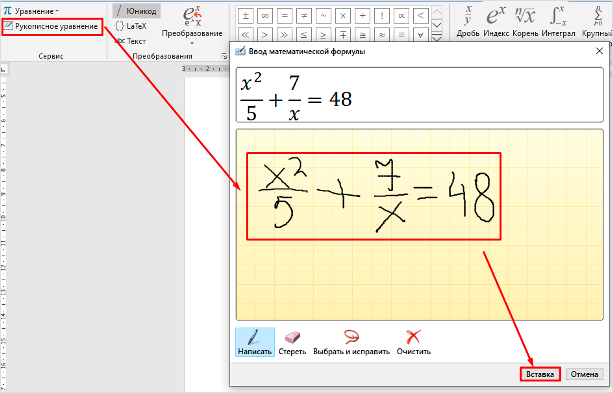
С доступными математическими символами мы уже знакомились, тут есть весь необходимый набор: от сложения и умножения до знака бесконечности и оператора “не равно”.

Чтобы раскрыть полный перечень и выбрать соответствующую категорию букв и знаков, нажмите сначала на стрелочку вниз, а затем на надпись “Основные математические символы”.

Идем дальше вправо по панели инструментов. Теперь посмотрим, какие типичные выражения встроены в программу:

• простые дроби;
• значения с одинарными и двойными индексами, что позволяет легко сделать не только математическую или физическую, но и химическую формулу;
• кубические, квадратные и любые другие корни;
• обычные, двойные, тройные и контурные интегралы (о последних я, к счастью, мало что знаю, а вы?);
• операторы суммы, произведения и пересечения (последний, насколько я понимаю, применяется для множеств);
• всевозможные скобки, которые позволяют, например, записывать системы уравнений;
• тригонометрические функции;
• диакритические знаки, которые могут быть вам знакомы, если вы изучали логику или дискретный анализ в институте;
• логарифмы и пределы;
• различные операторы, отличные от стандартных “умножить”, “сложить”, “равно”;
• матрицы – моя любимая тема из высшей математики.

Все эти шаблоны собраны в подразделе “Структуры”.

Юникод и HTML-объекты

Другие варианты и связанные персонажи:

• U + 002A * ASTERISK (HTML   · )
• U + 2062 НЕВИДИМЫЕ ВРЕМЯ (HTML   · ) (пробел нулевой ширины, указывающий на умножение)
• U + 00B7 · СРЕДНЯЯ ТОЧКА (HTML   · ) ( интерпункт может быть легче набирать, чем оператор точки)
• U + 2297 ⊗ КРУГЛЫЕ ВРЕМЕНИ (HTML   · )
• U + 22C5 ⋅ ТОЧЕЧНЫЙ ОПЕРАТОР (HTML   · )
• U + 2715 ✕ УМНОЖЕНИЕ X (HTML )
• U + 2716 ТЯЖЕЛОЕ УМНОЖЕНИЕ X (HTML )
• U + 2A09 ⨉ N-ARY TIMES OPERATOR (HTML )
• U + 2A2F ⨯ ВЕКТОР ИЛИ ПЕРЕКРЕСТНОЙ ПРОДУКТ (HTML   · ) (предназначен для явного обозначения перекрестного произведения двух векторов)
• U + 2A30 ⨰ ЗНАК УМНОЖЕНИЯ С ТОЧКОЙ ВЫШЕ (HTML   · )
• U + 2A31 ⨱ ЗНАК УМНОЖЕНИЯ С ПОДЧИНОЙ (HTML   · )
• U + 2A34 ⨴ ЗНАК УМНОЖЕНИЯ В ЛЕВОЙ ПОЛОВИНЕ КРУГА (HTML   · )
• U + 2A35 ⨵ ЗНАК УМНОЖЕНИЯ В ПРАВОЙ ПОЛОВИНЕ (HTML   · )
• U + 2A36 ⨶ КРУГЛЫЙ ЗНАК УМНОЖЕНИЯ С CIRCUMFLEX ACCENT (HTML   · )
• U + 2A37 ⨷ ЗНАК УМНОЖЕНИЯ В ДВОЙНОМ КРУГЕ (HTML   · )
• U + 2A3B ⨻ ЗНАК УМНОЖЕНИЯ В ТРЕУГОЛЬНИКЕ (HTML   · )
• U + 2AC1 ⫁ ПОДСТАВКА СО ЗНАКОМ УМНОЖЕНИЯ НИЖЕ (HTML   · )
• U + 2AC2 ⫂ SUPERSET С ЗНАКОМ УМНОЖЕНИЯ НИЖЕ (HTML   · )

Как умножать в экселе

• Как умножать в экселе
• Как в excel умножить столбцы
• Как считать в Экселе (Excel)

Табличный редактор Excel 2007

Если требуется разовое действие – перемножить два числа – то последовательность действий должна быть такой:

– перейдите в пустую ячейку таблицы Excel (можно с помощью навигационных клавиш-стрелок, а можно щелкнув нужную ячейку мышью);

– нажмите клавишу “=”. Excel интерпретирует это действие как начало ввода формулы;

– теперь печатайте нужное вам математическое действие, используя в качестве знака умножения звездочку (*). Знаки математических действий принято назвать «операторами». Например, если надо перемножить 2 на 3, то в ячейке вам нужно напечатать “=2*3” – здесь знак равенства остался от предыдущего шага, повторно печатать его не нужно. Если требуется перемножить не два, а больше чисел – ничего не меняется в правилах, печатайте больше. Например, =2*3*4*7*12;

– по завершению ввода нажмите Enter. Excel рассчитает результат и покажет его в этой же ячейке.

Вместо обычной записи математического действия с использованием оператора умножения (*), можно использовать функцию с именем ПРОИЗВЕД. В этом случае содержимое ячейки таблицы, осуществляющей перемножение пяти чисел, будет выглядеть так: =ПРОИЗВЕД(2;3;4;7;12).

Если надо организовать постоянную форму из нескольких ячеек, чтобы в одной из них напечатать множимое, в другой – множитель, а в третьей увидеть результат умножения:

– в первой свободной ячейке напечатайте число (множимое) и нажмите Enter;

– во второй свободной ячейке напечатайте второе число (множитель) и нажмите Enter;

– в третьей ячейке нажмите клавишу “=” и с помощью клавиш навигации (стрелок) переместитесь в первую ячейку (содержащую множимое). Можно вместо клавиш просто щелкнуть ячейку курсором мыши. Сделав это, нажмите звездочку (оператор умножения). При этом курсор вернется обратно в третью ячейку, а вам нужно с помощью тех же клавиш навигации или курсора мыши перейти во вторую ячейку, содержащую множитель. После этого содержимое ячейки с формулой должно выглядеть, например, так: =A1*A2. Сделав все это, нажмите Enter для завершения ввода формулы и в третьей ячейке увидите результат умножения.

Вы построили мини-калькулятор – теперь можете менять числа множимого и множителя, а Excel будет в третьей ячейке показывать их произведение.

И здесь умножаемых чисел не обязательно должно быть только два, действуя точно так же можно организовать нужное вам количество перемножаемых ячеек с числами. Но в этом случае удобнее будет пользоваться не оператором *, а функцией ПРОИЗВЕД. Тогда вам не надо будет указывать каждую ячейку с числом по отдельности, а можно указать целый диапазон ячеек. Например, если вы поместили перемножаемые числа в ячейки начиная с A1 и заканчивая A8, то содержимое ячейки, показывающей результат перемножения их всех, должно быть таким: =ПРОИЗВЕД(A1:A8). Диапазон ячеек можно вписать в функцию «вручную», а можно выделить мышью и Excel впишет нужные значения сам.

Если надо разово умножить значение каждой ячейки в столбце (или строке) таблицы на какой-то коэффициент:

– в пустой ячейке напечатайте это число-коэффициент;

– затем выделите эту ячейку, на вкладке «Главная» в самой первой группе («Буфер обмена») нажмите кнопку «Копировать»;

– теперь выделите диапазон ячеек, которые требуется умножить на коэффициент. Это можно сделать как мышкой, так и с помощью стрелок при нажатой клавише CTRL;

– в той же группе «Буфер обмена», ниже команды «Вставить», есть стрелка, которая открывает дополнительные варианты вставки – щелкните ее и выберите в списке пункт «Специальная вставка»;

– в группе переключателей «Операция» выберите «Умножить»;

– нажмите кнопку «ОК» и Excel перемножит каждую выделенную ячейку на значение коэффициента, скопированного вами в буфер обмена.

Как вставить формулу в таблицу в Word

В этой статье мы рассмотрим, как вставить формулу в таблицу в ворде.

Microsoft Word позволяет использовать математические формулы в ячейках таблицы, которые могут использоваться для суммирования чисел, для поиска среднего значения, или нахождения наибольшего или наименьшего числа в указанных ячейках таблицы. Существует список формул, которые вы можете использовать для вычислений в таблице в ворде.

Как вставить формулу в таблицу

Ниже приведены простые шаги для вставки формулы в ячейку таблицы в ворде:

1. В нашем примере рассмотрим следующую таблицу, в которой нам необходимо посчитать сумму строк. Для того чтобы вставить формулу в таблицу в ворде, сперва установите курсор в ячейке таблицы.

1. Перейдите на вкладку «Макет» и нажмите кнопку «Формула».

Как вставить формулу в таблицу в Word – Вставка формулы в таблице

1. Откроется диалоговое окно «Формула», в котором в поле «Формула» будет предложена формула по умолчанию SUM(LEFT).

   Данная формула посчитает сумму значений, находящихся в ячейках справа от ячейки, где находится формула. В нашем случае эта формула идеально подходит.

В поле «Формат числа:» вы можете выбрать формат числа, из списка предложенных форматов.

А с помощью поля «Вставить функцию:» вы можете изменить формулу, используя список доступных функций.

Как вставить формулу в таблицу в Word – Функции

1. Теперь нажмите «OK», чтобы применить формулу, и вы увидите, что левые ячейки были просуммированы, и результат был помещен в ячейку, где мы и хотели.

Как вставить формулу в таблицу в Word – Результат формулы суммы ячеек в таблице в ворде

1. Повторите действия для остальных ячеек, чтобы посчитать сумму остальных строк.
2. Если числовые значения в ячейках были изменены, формула автоматически не пересчитывается.

   Для того чтобы обновить значение расчета формулы в таблице в ворде, щелкните правой кнопкой мыши по значению и выберите пункт «Обновить поле».

Формулы ячеек в таблице

Рассмотрим следующие основные функции, которые можно использовать, для того чтобы вставить формулу в ячейке таблице в ворде.

№	Формула	Описание
1	AVERAGE( )	Среднее значение
2	COUNT( )	Количество элементов
3	MAX( )	Наибольшее значение
4	MIN( )	Наименьшее значение
5	PRODUCT( )	Произведение элементов
6	SUM( )	Сумма элементов

Для вставки формул в таблицу в Word используется тот же принцип обращения к отдельным ячейкам, как и в электронных таблицах Excel.

Каждый столбец идентифицируется буквой, начиная с A для первого столбца, B для второго столбца и так далее. После буквы вводится номер строки.

Таким образом, первая ячейка в первой строке равна A1, третья ячейка в четвертой строке – C4 и так далее.

Ниже приведена таблица, в которой представлены способы обращения к ссылкам на ячейки, для использования вставки формулы в таблице в ворде.

№	Ссылки на ячейки и описание
1	Одна ссылка на ячейку, например, B3 или F7.
2	Диапазон ячеек, например, A2:A5 или C7:C15.
3	Ряд отдельных ячеек, например, A3; B4; C5.
4	ABOVE, ссылка ко всем ячейкам в столбце выше текущей ячейки.
5	BELOW, ссылка ко всем ячейкам в столбце ниже текущей ячейки.
6	LEFT, ссылка на все ячейки в строке слева от текущей ячейки.
7	RIGHT, ссылка на все ячейки в строке справа от текущей ячейки.

Вы также можете создавать простые математические формулы, такие как B3+B5*10, используя простые математические операторы +, -, /, *,%.

Ну вот, надеюсь, что вопрос, как вставить формулу в таблицу в ворде, у вас больше не возникнет, и вы будете использовать автоматические вычисления в таблицах в ворде.

Решение вирусных школьных математических задач с опущенным знаком умножения

Я не буду рассматривать все варианты, предложенные в интернете, а просто покажу, какими правилами необходимо руководствоваться при решении подобных вирусных математических задач.

Первым действием, с чем никто не спорит, находится выражение в скобках. Получаем:

1) \(2+2=4\).

А вот дальше начинается самое интересное. Загвоздка подобных задач, приводящая к их неоднозначному толкованию, заключается в опущенном знаке умножения.

Столкновение мнений происходит из-за того, что кто-то забыл, что означает пропущенный знак умножения между числом и скобкой, кто-то не понял это в свое время, а у кого-то это вообще прошло мимо.

Пункт 3 в списке случаев, когда возможно опустить знак умножений, нам говорит, что это допускается . А если есть явное указание на существование одного из множителей, значит существует, как минимум, ещё один множитель, а именно: выражение в скобках.

Предположим, что в данной задаче главное – это последовательность совершения действий, на чем настаивают некоторые комментаторы задачи, и после вычисления суммы в скобках нужно выполнить действия второй ступени: сперва деление 8 на 2, потом умножение 4 на 4. Но тогда получается, что в записи \(8\div 2(2+2)\) знак умножения пропущен между делителем 2 и скобкой (2+2), что является нарушением правил опускания знака умножения, и такая трактовка условия . Для корректного представления частного \(8\div 2\), оно должно было быть заключено в скобки следующим образом: \((8\div 2)(2+2)\).

Следовательно, мы можем рассматривать 2 перед скобкой только как множитель, 8 – это, безусловно, делимое, а делителем выступает выражение, представленное произведением \(2 \times (2+2)\). Само выражение \(8\div 2\times (2+2)\) при этом – это деление числа на произведение, где 2 – это первый множитель, а \((2+2)\) – это второй множитель.

Получается, полностью понятная запись этой задачи, тождественная исходной и не вызывающая разночтений, выглядит так:

\(8\div \).

Корректность начального условия задачи и преобразования его при помощи скобок в такой вид я покажу чуть ниже.

А найти результат деления числа на произведение можно двумя способами:1) делимое число разделить на результат произведения;2) делимое разделить на первый множитель произведения, результат разделить на второй множитель и т.д.

Поэтому, решения этой задачи – нахождение произведения первого множителя 2 и второго, представляющего собой сумму выражения в скобках:

2) \(2\times 4=8\).

Остается только выполнить третье действие – найти частное от деления 8 на 8:

3) \(8\div 8=1\).

Итак, результат решения задачи:

\(8\div 2\times (2+2)=1\).

Подтверждением правильности исходной записи задачи и ее преобразования в полностью понятный вид является практика правописания алгебраических выражений: при записи деления числа на произведение, в котором были опущены знаки умножения, скобки, заключающие в делителе число, выраженное произведением, также обычно опускаются. То есть:\(a\div ( k\times l\times m)=a\div (klm)=a\div klm\).

А в нашем случае мы имеем результат этой записи, то есть, в делителе, который выражен произведением с опущенным знаком умножения, были опущены скобки. И нам следует выполнить обратные действия, то есть: восстановить опущенные скобки и знак умножения. Тогда наш изначальный пример приобретет такой вид, тождественный начальному:

\(8\div \).

Да, вирусные примеры с опущенным знаком умножения специально записываются таким образом, который предполагает возникновение разночтения у людей с разной математической подготовкой. И без знания правил и четкого их понимания выпутаться практически невозможно.

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

1. Умножая 3029 на 9, находим:

    3029
   ×   9 
   27261 первое частное произведение

2. Умножая 3029 на 20, находим:

    3029
   ×   20 
    60580 второе частное произведение

3. Умножая 3026 на 400, находим:

    3029
   ×   400 
   1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

1. нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.

2. Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.

3. Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.

4. Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.