Функции и методы модуля math в python. математические функции в python

Присвоение типа переменной

Работа с числами в Python должна осуществляться исключительно с переменными, которые являются числовыми. То есть, если в переменных строчного типа будет число, то ее нельзя добавить к числу, чтобы получить сумму. Для этого необходимо предварительно перевести такую строку в числовой формат. 

Это делается с помощью двух функций. Также мы рассмотрим третью функцию, которая выполняет обратную операцию – переводит число в строку. Это также связано с нашей темой, поскольку это действие, которое мы осуществляем с числами.

Для преобразования одного типа переменных в другой используются специализированные переменные, которые называются конструкторами.

Первая переменная – это int(). Она используется для того, чтобы превратить строку или число с плавающей точкой в целочисленную переменную. Это делается путем непосредственного преобразования для строки или с помощью отсекания дробной части у числа с плавающей точкой. 

Приведем пример использования функции int() для разных задач. 

x = int(1) # x станет 1  

y = int(2.8) # y станет 2  

z = int("3") # z станет 3

В первом случае используется обычное целочисленное значение в качестве аргумента. В этом случае функция вернет это же самое целочисленное значение. Такой подход используется для того, чтобы указать конкретный тип переменной и предотвратить ошибочное его присвоение. На практике же, необходимость в этом бывает довольно редко.

Во втором случае мы присвоили функции int() значение 2.8. Видим, что само это число имеет в дробной части цифру 8, которая должна была бы округляться таким образом, чтобы в целочисленной части стало 3. Но на практике мы видим, что станет 2 в этом случае. То есть, округление происходит не по правилам. 

И, наконец, в этом примере мы использовали строку ‘3’ для того, чтобы переменная z стала целочисленной.

Для преобразования строки или целочисленного значения в число с плавающей точкой используется функция float(). Она создает число с плавающей точкой из целочисленного значения типа 34.0. Если строка состоит исключительно из числа с плавающей точкой, эта функция может его конвертировать в соответствующий тип данных.

Приведем пример кода, демонстрирующего разные особенности использования этой функции. 

x = float(1) # x станет 1.0  

y = float(2.8) # y станет 2.8  

z = float("3") # z станет 3.0  

w = float("4.2") # w станет 4.2

Видим, что в первой строке число, передаваемое в качестве аргумента функции float(), целочисленное. В этом случае оно превращается в число с плавающей точкой, где в дробной части написан ноль. То есть, 1.0.

С дробными частями и со строками все понятно

Только обратите внимание, что можно использовать как строки с целочисленными значениями в качестве аргументов. В этом случае логика такая же самая

Фактически строка конвертируется в целочисленное значение, а потом конвертируется в дробное.

Отдельно поговорим о функции str(). Хотя она не имеет непосредственного отношения к нашей теме, ее приходится часто использовать для чисел. Например, для создания строки, включающей число, которое получилось в результате вычислений. И хотя в большинстве случаев Python все делает самостоятельно и правильно, иногда приходится вручную задавать тип данных.

Приведем три примера, как разные типы данных конвертируются в строки

Обратите внимание, что функции str() можно также передавать строчные данные. 

x = str("s1") # x станет 's1'  

y = str(2) # y станет '2'  

z = str(3.0) # z станет '3.0'

Модуль random

Модуль random предоставляет функции для генерации случайных чисел, букв, случайного выбора элементов последовательности. Модуль собрал разные функции для
имитации случайных процессов: , , , , ,
и другие.

Задание 4.3 Камень, ножницы, бумага

Запрограммируйте игру с компьютером в «Камень, ножницы, бумага». Пример диалога:

Счет 0:0
Ваш ход (0-выход, 1-камень, 2-ножницы, 3-бумага): 1
Мой ход: 2
Вы выиграли!
Счет 0:1
Ваш ход (0-выход, 1-камень, 2-ножницы, 3-бумага): 3
Мой ход: 3
Ничья!
Счет 0:1
Ваш ход (0-выход, 1-камень, 2-ножницы, 3-бумага): 1
Мой ход: 3
Вы проиграли!
Счет 1:1
Ваш ход (0-выход, 1-камень, 2-ножницы, 3-бумага): 0
Игра окончена со счетом 1:1

7.1.1. Значения -inf, inf и nan

Возможно вы обратили внимание на то, что когда мы вычисляли натуральный логарифм массива, среди значений которого был ноль, не появилось абсолютно никакой ошибки, а сам логарифм стал равен значению -inf (минус бесконечность). Убедимся в этом еще раз:. Более того, в NumPy мы даже можем делить на ноль:

Более того, в NumPy мы даже можем делить на ноль:

NumPy предупредил нас о том, что встретил деление на ноль, но тем не менее выдал ответ inf (плюс бесконечность). Дело в том, что с математической точки зрения все абсолютно верно — если вы что-то делите на бесконечно малое значение то в результате получете значение, которое окажется бесконечно большим. Если результатом математической операции является плюс или минус бесконечность, то логичнее выдать значение inf или -inf чем выдавать ошибку.

В NumPy есть еще одно специальное значение — nan . Данное значение выдается тогда, когда результат вычислений не удается определить:

Заметьте, что NumPy нас просто предупредил о том, что ему попалось недопустимое значение, но ошибки не возникло. Дело в том, что в реальных вычислениях значения nan , inf или -inf встречается очень часто, поэтому появление этого значения проще обрабатывать специальными методами (функции numpy.isnan() и numpy.isinf() ), чем постоянно лицезреть сообщения об ошибках.

Новичкам, довольно трудно привыкнуть, к тому что в недрах компьютера вся арифметика на самом деле является двоичной и с этим связано очень много казусов. Во первых не совсем понятно, когда ждать появления значений -inf и inf :

Число 1.633123935319537e+16 появилось потому что в NumPy выполняются арифметические, а не символьные вычисления, т. е. число π хранится в памяти компьютера не как знание о том, что это математическая константа с бесконечным количеством десятичных знаков после запятой, а как обычное число с десятичной точкой (десятичная дробь) равная числу π с очень маленькой, но все же, погрешностью:

NumPy отличает предельные случаи, когда вычисления выполнить невозможно, например, деление на ноль. В таких случаях появляются значения -inf , inf и nan . Если из-за самых незначительных погрешностей вычисления все же возможны, то NumPy их обязательно выполнит. В этих случаях вместо значений -inf или inf у вас будут появляться самые маленькие или самые большие числа, которые возможно представить на вашем компьютере.

Тем не менее и на этом сюрпризы не заканчиваются. Если число 1.633123935319537e+16 является самым больши, которое может появиться при вычислениях, оно вполне ожидаемо должно появиться в самых разных ситуациях. Например:

То, есть какая-то, длинная арифметика все же доступна — очень хорошая новость, для лбителей криптографии и теории чисел. Но иногда:

В заключение могу лишь сказать, что все предельные случаи требуют кардинальных решений. Некоторые решения имеются в самом NumPy, некоторые предоставляют другие пакеты. Если вам необходимы точные решения, то лучше обратиться к системам компьютерной алгебры и символьных вычислений, например пакету SymPy — маленький, но мощьный пакет Python для символьных вычислений. Если вы решили отправиться в самые дебри теории чисел, алгебры и криптографии, то лучшим решением окажется программа GAP. Программа GAP не является программой Python, но имеет Python интерфейс в замечательной программе Sage, которая определенно заслуживает вашего внмания.

Показатели и логарифмы

В этом разделе мы рассмотрим функции библиотеки Math, используемые для поиска различных типов показателей и логарифмов.

Функция exp()

Математическая библиотека в Python поставляется с функцией exp(), которую мы можем использовать для вычисления степени e. Например, e x , что означает экспоненту от x. Значение e составляет 2,718281828459045.

Метод можно использовать со следующим синтаксисом:

math.exp(x)

Параметр x может быть положительным или отрицательным числом. Если x не является числом, метод вернет ошибку. Продемонстрируем использование этого метода на примере:

import math

# Initializing values
an_int = 6
a_neg_int = -8
a_float = 2.00

# Pass the values to exp() method and print
print(math.exp(an_int))
print(math.exp(a_neg_int))
print(math.exp(a_float))

Вывод:

403.4287934927351
0.00033546262790251185
7.38905609893065

Мы объявили три переменные и присвоили им значения с разными числовыми типами данных. Затем мы передали их методу exp() для вычисления их показателей.

Мы также можем применить этот метод к встроенным константам, как показано ниже:

import math

print(math.exp(math.e))
print(math.exp(math.pi))

Вывод:

15.154262241479262
23.140692632779267

Если вы передадите методу нечисловое значение, он выдаст ошибку, как показано здесь:

import math

print(math.exp("20"))

Вывод:

Traceback (most recent call last):
  File "C:/Users/admin/mathe.py", line 3, in <module>
    print (math.exp("20"))
TypeError: a float is required

Ошибка TypeError была сгенерирована, как показано в приведенных выше выходных данных.

Функция log()

Эта функция возвращает логарифм указанного числа. Натуральный логарифм вычисляется по основанию e. Следующий пример демонстрирует использование этой функции:

import math

print("math.log(10.43):", math.log(10.43))
print("math.log(20):", math.log(20))
print("math.log(math.pi):", math.log(math.pi))

В приведенном выше скрипте мы передали методу числовые значения с разными типами данных. Мы также вычислили натуральный логарифм константы пи. Результат выглядит так:

Вывод:

math.log(10.43): 2.344686269012681
math.log(20): 2.995732273553991
math.log(math.pi): 1.1447298858494002

Функция log10()

Этот метод возвращает десятичный логарифм указанного числа. Например:

import math

# Returns the log10 of 50
print("The log10 of 50 is:", math.log10(50))

Вывод:

The log10 of 50 is: 1.6989700043360187

Функция log2()

Эта функция вычисляет логарифм числа по основанию 2. Например:

import math

# Returns the log2 of 16
print("The log2 of 16 is:", math.log2(16))

Вывод:

The log2 of 16 is: 4.0

Функция log (x, y)

Эта функция возвращает логарифм x, где y является основанием. Например:

import math

# Returns the log of 3,4
print("The log 3 with base 4 is:", math.log(3, 4))

Вывод:

The log 3 with base 4 is: 0.6309297535714574

Функция log1p (x)

Эта функция вычисляет логарифм (1 + x), как показано здесь:

import math

print("Logarithm(1+x) value of 10 is:", math.log1p(10))

Вывод:

Logarithm(1+x) value of 10 is: 2.3978952727983707

Сложные числа

Python – один из немногих языков программирования, который обеспечивает встроенную поддержку комплексных чисел. Хотя комплексные числа не часто возникают за пределами области научных вычислений и компьютерной графики, поддержка их Python является одной из его сильных сторон.

Если вы когда-либо проходили курс предварительного вычисления или математической алгебры более высокого уровня, то, возможно, помните, что комплексное число – это число с двумя различными компонентами: действительной и мнимой частью.

Чтобы создать комплексное число в Python, вы просто пишете действительную часть, затем знак плюс, затем мнимую часть с буквой в конце:

Когда вы проверите значение , вы заметите, что Python заключает число в круглые скобки:

Это соглашение помогает избежать путаницы, связанной с тем, что отображаемый результат может представлять собой строку или математическое выражение.

Мнимые числа имеют два свойства, и , которые возвращают действительную и мнимую составляющие числа соответственно:

Обратите внимание, что Python возвращает как действительные, так и мнимые компоненты как числа с плавающей запятой, даже если они были указаны как целые числа. У комплексных чисел также есть метод , который возвращает комплексное сопряжение числа:

У комплексных чисел также есть метод , который возвращает комплексное сопряжение числа:

Для любого комплексного числа его сопряжение – это комплексное число с одинаковой действительной и мнимой частью, одинаковое по модулю, но с противоположным знаком. Итак, в этом случае комплексное сопряжение равно .

За исключением оператора floor division (), все арифметические операторы, которые работают с числами с плавающей запятой и целыми числами, также будут работать с комплексными числами. Поскольку это не углубленное изучение математики, мы не будем обсуждать механику сложной арифметики. Вместо этого вот несколько примеров использования комплексных чисел с арифметическими операторами:

Интересно, хотя и не удивительно с математической точки зрения, объекты и также имеют свойства и , а также метод :

Для чисел с плавающей запятой и целых чисел и всегда возвращают само число, а всегда возвращает 0. Однако следует отметить, что и возвращают целое число, если является целым числом и число с плавающей запятой, если – число с плавающей точкой.

Теперь, когда вы познакомились с основами комплексных чисел, вы можете задаться вопросом, когда вам когда-нибудь понадобится их использовать. Если вы изучаете Python для веб-разработки, анализа данных или программирования общего назначения, правда в том, что вам никогда не придется использовать комплексные числа.

С другой стороны, комплексные числа важны в таких областях, как научные вычисления и компьютерная графика. Если вы когда-либо работали в этих областях, вам может пригодиться встроенная в Python поддержка комплексных чисел.

Типы чисел в Python

Итак, каждый тип чисел в Python кодируется отдельным словом. За целочисленный формат отвечает int(), за числа с плавающей точкой (десятичные дроби, то есть) – float. Отдельно от них стоят комплексные числа, понять которые довольно непросто.

Но начнем с самого простого – с целочисленных значений. Это тип Integer, который в большом количестве языков программирования так и записывается. В Python указывается сокращенное название – int, но принципиальных отличий от других в этом вопросе нет. 

Переменная целочисленного типа объявляется таким же образом, как и любая другая. Необходимо написать ее название, а потом с помощью оператора присваивания дать ей значение. 

x = 1 # int 

Числа с плавающей точкой – это привычные нам десятичные дроби. Они получили такое название, потому что точка (или запятая) может стоять в любом месте. Перед ней может быть 10 чисел, а после нее – 20. Или же перед точкой может быть всего одно число, а вот после нее ряд стремится к бесконечности. 

В языке  Python разделение типов осуществляется настолько жестко, что иногда появляется необходимость конвертировать тип с плавающей точкой в стандартный целочисленный. Но об этом дальше.

Самый тяжелый для понимания тип – это комплексные числа. Тяжело разобраться в их особенностях потому, что они не являются понятными. Нельзя их аналогов найти в реальном мире. По крайней мере, в осязаемой его части. Тем не менее, они активно используются в целом спектре областей человеческой деятельности.

Запись комплексных чисел осуществляется с использованием буквы j. Как в этом примере.

z = 1j # complex

Int

В качестве переменной этого типа могут использоваться не только натуральные числа, но и отрицательные значения. Длина числа может быть любой. Главное требование – отсутствие десятичных знаков.  

x = 1  

y = 35656222554887711  

z = -3255522    

print(type(x))  

print(type(y))  

print(type(z))

Собственно, вывод интерпретатора здесь будет следующим. 

<class 'int'>

<class 'int'>

<class 'int'>

Float

Этот тип данных являет собой число с плавающей точкой. Приведем несколько примеров с выводом консоли интерпретатора. 

x = 1.10  

y = 1.0  

z = -35.59  

print(type(x))  

print(type(y))  

print(type(z))

Этот фрагмент кода объявляет три переменные, присваивает им значения чисел с плавающей точкой (включая отрицательные и аналоги целым числам типа 1.0), а потом определяет тип данных этих переменных и выводит в консоль. 

Собственно, вывод будет следующим. 

<class 'float'>

<class 'float'>

<class 'float'>

Число экспоненциального формата (то бишь, с e) также относится к этому типу, если в нем указывается степень десятичности. 

Комплексные числа

Если говорить просто, то это двухмерные числа. Хотя среднестатистическому начинающему разработчику Python от этого более понятно не становится. Если говорить более понятно, то для обычного числа можно нарисовать прямую, и есть закономерность – справа находятся большие значения. А вот комплексные числа уже требуют плоскости и новых определений того, что является большим или меньшим. 

Если выражать в формуле, то комплексное число являет собой такое, которое представлено в виде a + bi, где в качестве i выступает мнимая единица (ее квадрат равен -1). 

Работа с комплексными числами в Python осуществляется с использованием буквы j. Приведем пример кода, в котором это реализовано на практике. 

x = 3+5j  

y = 5j  

z = -5j  

print(type(x))  

print(type(y))  

print(type(z))

Если запустить эту программу, то интерпретатор выведет следующие строки. 

<class 'complex'>

<class 'complex'>

<class 'complex'>

Дополнительные методы и операции в Python

В эти операции входят:
• int.bit_length() — количество бит, которое необходимо, чтобы представить число в двоичном виде без учёта лидирующих нулей и знака;
• int.to_bytes(length, byteorder, *, signed=False) — метод возвращает строку байтов, которые представляют это число;
• classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращение числа из заданной строки байтов.

Пример работы последнего метода:

>>>
>>> int.from_bytes(b'\x00\x10', byteorder='big')
16
>>> int.from_bytes(b'\x00\x10', byteorder='little')
4096
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True)
-1024
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False)
64512
>>> int.from_bytes(, byteorder='big')
16711680

Способы извлечения корня

В языке программирования Python 3 существует три способа извлечения корней:

• Использование функции sqrt из стандартной математической библиотеки math.
• Операция возведения в степень **
• Применение функции pow(x, n)

Чтобы воспользоваться первым способом, необходимо вначале импортировать sqrt из модуля math. Это делается с помощью ключевого слова import: . При помощи этой функции можно извлекать только квадратный корень из числа. Приведем пример:

from math import sqrt
x = sqrt(4)
print(x)

2.0

Если же нам нужно вычислить в Python корень квадратный из суммы квадратов, то можно воспользоваться функцией hypot из модуля math. Берется сумма квадратов аргументов функции, из нее получается корень. Аргументов у функции два.

from math import hypot
x = hypot(4,3)
print(x)

5.0

Еще одним, чуть более универсальным методом, будет использование возведения в степень. Известно, что для того, чтобы взять корень n из числа, необходимо возвести его в степень 1/n. Соответственно, извлечение квадратного корня из числа 4 будет выглядеть так:

n = 2
x = 4**(1./n)
print(x)

2.0

Обратите внимание, что в Python 2 необходимо ставить точку после единицы, иначе произойдет целочисленное деление, и 1/n == 0, а не нужной нам дроби. В Python 3 можно не ставить точку.. Последний метод использует функцию pow(value, n)

Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа

Последний метод использует функцию pow(value, n). Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа.

x = pow(4, 0.5)
print(x)

2.0

Какой метод быстрее?

Для того, чтобы определить какой же метод предпочтительнее использовать, напишем программу. Замерять время выполнения будем с помощью метода monotonic библиотеки time.

from time import monotonic
from math import sqrt
iterations = 1000000
start = monotonic()
for a in range(iterations):
    x = sqrt(4)
print("sqrt time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
    x = 4 ** 0.5
print("** time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
    x = pow(4, 0.5)
print("pow time: {:>.3f}".format(monotonic() - start) + " seconds")

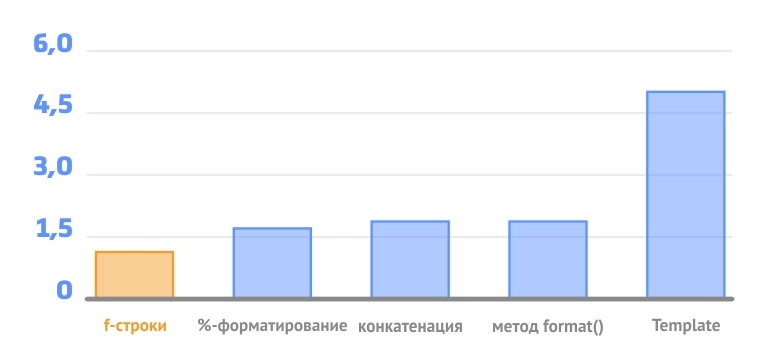
sqrt time: 0.266 seconds
** time: 0.109 seconds
pow time: 0.453 seconds

Как видно, самое быстрое решение — использовать **. На втором месте метод sqrt, а pow — самый медленный. Правда, метод sqrt наиболее нагляден при вычислении в Python квадратных корней.

Таким образом, если критична скорость, то используем **. Если скорость не критична, а важна читаемость кода, то следует использовать sqrt.

Числа и арифметика в Python

Мы уже видели пример переменной, содержащей число выше:

«Число» — неформальное название для такого рода вещей, но если мы хотим быть более техническими, мы можем спросить Python, как он описывает тип вещи, которым является :

Здесь — сокращение от integer. Есть еще один вид чисел, с которым мы часто сталкиваемся в Python:

— это число с плавающей точкой, которое очень полезно для представления таких вещей, как вес или пропорции.

— еще одна встроенная функция, которую мы встречаем (после ), и ее следует запомнить. Очень полезно иметь возможность спросить Python «к какому типу вещей относиться это?».

Естественное желание действий с числами — выполнять арифметические операции. Мы видели оператор для сложения и оператор для умножения. Python также покрывает остальные основные кнопки вашего калькулятора:

Оператор	Название	Описание
	Сложение	Сумма и
	Вычитание	Разница и
	Умножение	Произведение и
	Истинное деление	Частное и
	Деление с округлением	Частное и , без дробных частей
	Модуль	Целочисленный остаток от деления на
	Возведение в степень	в степени
	Отрицание	Противоположное к

Одно интересное наблюдение заключается в том, что, в то время как ваш калькулятор, вероятно, имеет только одну кнопку для деления, Python может выполнять два вида. «Истинное деление» — это именно то, что делает ваш калькулятор:

Это всегда дает нам .

Оператор дает результат, который округляется вниз до целого числа.

Вы можете придумать, где это будет полезно?

Порядок действий

В арифметике, которую мы изучали в школе, есть соглашения о порядке, в котором выполняются операции. В англоязычной литературе можно встретить технику запоминания порядка с помощью мнемоники, такой как PEMDAS — скобки, возведение в степень, умножение/деление, сложение/вычитание (Parentheses, Exponents, Multiplication/Division, Addition/Subtraction).

Python следует аналогичным правилам относительно того, какие вычисления выполнять в первую очередь. В основном они интуитивно понятны.

Иногда порядок операций по умолчанию не соответствует нашему желанию:

Здесь вам пригодятся круглые скобки. Вы можете добавить их, чтобы Python вычислял подвыражения в необходимом вам порядке.

Встроенные функции для работы с числами

Функции и возвращают минимум и максимум своих аргументов соответственно:

Функция возвращает абсолютное значение своего аргумента:

Помимо имен двух основных числовых типов Python, и также могут вызываться как функции, которые преобразуют свои аргументы в соответствующий тип:

Решение реальной задачи с использованием sqrt

Корень – дитя геометрии. Когда Пифагор доказал свою знаменитую теорему, людям тут же захотелось вычислять стороны треугольников, проверять прямоту внешних углов и сооружать лестницы нужной длины.

Соотношение a2 + b2 = c2, где «a» и «b» – катеты, а «c» – гипотенуза – естественным образом требует извлекать корни при поиске неизвестной стороны. Python-а под рукой у древних греков и вавилонян не было, поэтому считать приходилось методом приближений. Жизнь стала проще, но расчет теоремы Пифагора никто не отменял и в XXI веке.

Решим задачку про вышку сотовой связи. Заказчик требует рассчитать высоту сооружения, чтобы радиус покрытия был 23 километра. Мы неспешно отходим на заданное расстояние от предполагаемого места строительства и задумчиво смотрим под ноги. В голове появляются очертания треугольника с вершинами:

1. Ваше местоположение;
2. Центр Земли;
3. Пиковая высота вышки;

Модель готова, приступаем к написанию кода:

Расчёт выполнен, результат заказчику предоставлен. Можно идти пить чай и радоваться тому, что теперь ещё больше людей смогут звонить родным и сидеть в интернете.

Функция преобразования углов

У внимательного читателя мог на предыдущем этапе появиться вопрос: а что, если я не знаю, сколько радиан в угле? Я знаю только количество градусов. Ничего страшного, ведь библиотека math поддерживает возможность конвертации радиан в градусы и наоборот. 

Чтобы выполнить первую задачу, существует функция degrees(), которая принимает радиан в качестве аргумента и выводит количество градусов. 

Для того, чтобы получить количество радиан, зная количество градусов, следует воспользоваться функцией radians(), которая принимает величину угла в качестве аргумента.

Запомнить очень просто. То, что мы хотим получить, так и называется функция.

Битовые операторы

На практике, используются довольно редко. Но применяются. И знать их тоже надо. 

Для начала надо раскрыть, что такое побитовые операции в целом. Они выполняются над разрядами числа по специальным формулам, каждая из которых зависит от операторов.

Поэтому важно рассмотреть их более подробно. Бинарное И (&)

Полный аналог оператора and, только который работает с битами. Точно так же, как и любой другой битовый оператор, он выполняет операции с каждой парой битов по отдельности, осуществляя с ними действия в соответствии с этой таблицей

Бинарное И (&). Полный аналог оператора and, только который работает с битами. Точно так же, как и любой другой битовый оператор, он выполняет операции с каждой парой битов по отдельности, осуществляя с ними действия в соответствии с этой таблицей.

0 & 0 = 0

0 & 1 = 0

1 & 0 = 0

1 & 1 = 1

То есть, если первый бит в первой последовательности будет 0 и во второй последовательности битов первый бит будет 0, то после выполнения этой операции получится значение 0. 

Точно так же и с каждым последующим битом. Предположим, у нас есть две последовательности:

00100101

00111010

После того, как каждая из этих последовательностей битов будет обработана оператором, получится следующая последовательность:

00100000

Естественно, передавать значения можно и в десятичной форме. В таком случае они будут преобразованы в двоичную и выполнены соответствующие вычисления. А потом они снова будут преобразованы в десятичную систему. 

Например, если выполнить побитовое «И» с числами 2 и 3, то получится две последовательности битов в двоичной форме:

10

11

Если сопоставить с таблицей выше, то после побитового И будет выдан следующий результат:

10.

То есть, на вывод уйдет цифра 2, поскольку после выполнения операции побитового И 1 и 1 дали 1, а 0 и 1 дали 0. В результате, получилось значение 10, что соответствует 2.

По аналогичному принципу работают и другие бинарные операторы.

Бинарное ИЛИ (|). Соответствует побитовой операции or. 

Общая таблица сопоставления битов с использованием этого оператора следующая.

0 | 0 = 0

0 | 1 = 1

1 | 0 = 1

1 | 1 = 1

То есть, если ввести такую строку кода, получится на выходе 3.

>>> 2|3

Почему? Потому что эти две десятичные цифры переводятся в следующие две последовательности.

10

11

1 на 1 дает 1, и 0 на 1 дает 1. Соответственно, получилось число 11 в двоичной форме, что соответствует 3 в десятичной. Поэтому такой вывод.

Бинарное ИЛИ НЕТ (^). С помощью этой функции выполняется исключающее между двумя операндами, переведенными в двоичную форму. Сопоставление осуществляется по таким правилам.

0 ^ 0 = 0

0 ^ 1 = 1

1 ^ 0 = 1

1 ^ 1 = 0

Таким образом, если выполнить соответствующую операцию с теми же самыми числами, то получится в результате 1. Ведь цифра 2 у нас 10, а 11 – это 3. Таким образом, если сопоставить разряды по правилам, получится в итоге 01.

>>> 2^3

10

11

––

01

Инвертирующий оператор. С его помощью пользователь может инвертировать 0 в 1 и наоборот.

Например, если применить его к 2, то получится в результате -3. Почему? Потому что в двоичном формате цифра 2 – это 00000010. Если же ее инвертировать, то получится 11111101, что соответствует двоичной -3. Таким образом, получится в итоге обычная 2. 

Естественно, работает все и абсолютно наоборот. Ведь если 11111101 заменить на противоположные значения, то получится на выходе та же цифра 3.

Бинарный сдвиг влево и вправо. Осуществляет сдвиг левого оператора на ту позицию, которая есть справа. Например, если попробовать сдвинуть вправо бинарную 3 (то есть, 11) на два положения влево, то в результате получится число 00, поскольку единицы ушли за пределы разряда.

И такой принцип дальше. То есть, первый операнд – это то число, сдвиг которого надо осуществить. Второй же операнд – количество бит, на которое необходимо его выполнить.

Пример.

>>> 3>>2

>>> 3>>1

Условный оператор if

Оператор if позволяет изменить порядок выполнения операторов в зависимости от истинности или ложности некоторого условия. Формат оператора может быть записан в двух формах: полной и неполной форме.

if  условие:    # блок if    <операторы>else:    # блок else    <операторы>

Блок инструкций if будет выполнен, если условие истинно. Если условие ложно, будет выполнен блок инструкций else.

В условном операторе  может отсутствовать слово else и последующий блок. Такая инструкция называется неполным ветвлением.

Пример 5.  Записать следующее   выражение  на языке Python.Если a  >  0,  то  b  =  1,   иначе  a  =  0. 

print («Введите значение a: «) a = int(input())if a > :     b = 1       else:     b = print(«b = «, b)

Условный оператор  elif

if условие_1:   # блок if   <операторы>elif условие_2:   # первый блок elif   <операторы>elif условие_3:   <операторы>...else   # блок else   <операторы>   

Ключевое слово elifрасшифровывается, как else + if. Это конструкция позволяет  реализовать алгоритм  выбора   необходимого варианта из нескольких альтернативных вариантов.  Оператор elif позволяет упростить код. Сделать его легче читаемым и позволяет избежать написание несколько условий  if.

Когда исполняется инструкция if-elif-else, в первую очередь  проверяется условие_1.  Если условие истинно, тогда исполняется блок инструкций if .  Следующие условия и операторы пропускаются, и управление переходит к оператору  за  условным оператором if-elif-else.

Если условие_1 оказывается ложным, тогда управление переходит к следующему условию elif,  и проверяется условие_2.  Если оно истинно, тогда исполняются инструкции внутри первого блока elif. Последующие инструкции внутри этого блока пропускаются. Этот процесс повторяется, пока не находится условие elif, которое оказывается истинным. Если такого нет, тогда исполняется блок операторов else

 Пример.  

x = int(input())
y = int(input())if x > and y > print("Первая четверть")elif x > and y < print("Четвертая четверть")elif y > print("Вторая четверть")else: print("Третья четверть")