Math.round()
Содержание:
- Round(Decimal, MidpointRounding)
- Работа с таблицами Excel
- Округление результатов вычислений
- Правила округления десятичной дроби
- Правила округления
- Округление в Excel в меньшую сторону с помощью функции ОКРУГЛВНИЗ
- Неточные вычисления
- 32 Comments
- Excel. Формулы. Округление до кратного
- Точные правила округления чисел
- Использование функций округления
- Итого
Round(Decimal, MidpointRounding)
Math.Round(d, mode) rounds a decimal value to the nearest integer, and uses the specified rounding convention for midpoint values.
Syntax
The syntax of Round(d, mode) method is
Math.Round(Decimal d, MidpointRounding mode)
where
| Parameter | Description |
|---|---|
| d | The decimal number to be rounded. |
| mode | Specification for how to round the value if it is midway between two other numbers. |
Return Value
The method returns rounded Decimal value.
Example 4 – Round(Decimal, MidpointRounding)
In this example, we will take some decimal values and round them with different modes using Math.Round() method.
C# Program
using System;
class Example {
static void Main(string[] args) {
Decimal d, result;
d = 10.2M;
result = Math.Round(d, MidpointRounding.AwayFromZero);
Console.WriteLine($"Round({d}, MidpointRounding.AwayFromZero) = {result}");
d = 10.8M;
result = Math.Round(d, MidpointRounding.ToEven);
Console.WriteLine($"Round({d}, MidpointRounding.ToEven) = {result}");
d = 10.8M;
result = Math.Round(d, MidpointRounding.ToNegativeInfinity);
Console.WriteLine($"Round({d}, MidpointRounding.ToNegativeInfinity) = {result}");
d = 10.2M;
result = Math.Round(d, MidpointRounding.ToPositiveInfinity);
Console.WriteLine($"Round({d}, MidpointRounding.ToPositiveInfinity) = {result}");
d = 10.8M;
result = Math.Round(d, MidpointRounding.ToZero);
Console.WriteLine($"Round({d}, MidpointRounding.ToZero) = {result}");
}
}
Output
Round(10.2, MidpointRounding.AwayFromZero) = 10 Round(10.8, MidpointRounding.ToEven) = 11 Round(10.8, MidpointRounding.ToNegativeInfinity) = 10 Round(10.2, MidpointRounding.ToPositiveInfinity) = 11 Round(10.8, MidpointRounding.ToZero) = 10
Работа с таблицами Excel
Округление результатов вычислений
Существует ряд задач, для решения которых нет необходимости оперировать с большим количеством знаков после запятой. В частности, для работы с денежными единицами достаточно двух десятичных разрядов. В таком случае в определенных операциях (как промежуточных, так и производящих итоговые вычисления) необходимо выполнить округление результатов. Это может быть округление как до второго десятичного знака (скажем, до копеек, центов и т. д.), так и до целых значений. С этой целью используется функция округления, которая вводится посредством диалогового окна Мастер функций.
Рис. 2.28. Панель функции «ОКРУГЛ»
Данная функция округляет число до указанного количества десятичных разрядов. Синтаксис ее следующий:
ОКРУГЛ(число; количество_цифр) |
здесь число — это округляемое число, количество_цифр — это количество десятичных разрядов, до которого нужно округлить число.
Например, для операции извлечения корня в нашем примере формула округления будет иметь такой вид:
=ОКРУГЛ(В10/\(1/С10);2) |
Первый аргумент, В10/\(1/С10), показывает, для какой операции выполняется округление, а второй (цифра 2) определяет количество десятичных разрядов. В нашем случае вычисления осуществляются с точностью до второго знака после запятой (например, до копеек). Однако округление необходимо производить на определенном этапе расчетов.
ПРИМЕР: На таможню приходит товар стоимостью 3 цента за единицу в количестве 1000 штук. Курс обмена — 29,31 руб./$, а все таможенные платежи (без учета НДС) составляют 29,45%. База начисления для таможенных платежей будет равна цене в долларах, умноженной на курс доллара и количество единиц товара:
$0,03 * 29,31 * 1000 = 879,30 руб.
При умножении базы начисления на ставку таможенного сбора получается сумма, которой быть не может (так как не существует пока в мире десятых и сотых долей копеек при перечислении их через банк):
879,30 руб. * 29,45% = 258,9539 руб.
Если и далее производить расчеты без округления размера таможенного платежа, то можно получить стоимость партии товара, которая равна стоимости товара плюс таможенные платежи:
879,30 руб. + 258,9539 руб. = 1138,25385 руб.
Таким образом, цена единицы товара будет следующей:
1138,25385 руб. : 1000 шт. = 1,138254 руб.
Полученные неправильные результаты представлены в табл. 2.1.
| Цена за единицу ($) | Количество (штук) | Курс (руб./$) | Таможенный платеж (%) | Таможенный платеж (руб.) | Итого стоимость партии (руб.) | Цена за единицу (руб.) |
| 0,03 | 1000 | 29,31 | 29,45% | 258,9539 | 1138,25385 | 1,138254 |
Таблица 2.1. Пример неправильного расчета таможенных платежей
Поэтому некоторые значения следует округлить с точностью до копеек. А сумма таможенного платежа должна вычисляться по формуле
=ОКРУГЛ(цена в долларах х на курс доллара х количество;2) |
Цифра 2 означает, что выполняется округление с точностью до второго знака (то есть до копеек).
Таким же образом можно округлить и стоимость партии товара, в результате чего получится сумма, равная 1138,25 руб. Однако операция округления цены за единицу товара может привести к нежелательным последствиям. Это зависит от того, как происходит расчет цены. Если округлить цену товара до копеек, исходя из стоимости партии товара:
=ОКРУГЛ(1138,25/1000;2) |
то результат будет равен 1,14 руб. Но получается парадокс: произведя обратный расчет, мы получим, что партия стоит 1,14 * 1000 =1140 руб. Откуда-то взялись лишние 2 рубля. Эти 2 рубля могут значительно усложнить ведение бухгалтерского учета, если в бухгалтерской программе не предусмотрена возможность задания разрядности денежной единицы при некоторых операциях. До какого же знака целесообразно задать точность в данном примере?
В нашем случае точность округления должна быть равна разрядности копеек (2 знака после запятой) плюс разрядность числа, определяющего объем партии (у нас 3 разряда). Таким образом, необходимо округление до пятого знака.
| Цена ($) | Количество | Курс (руб./$) | Таможенный платеж (%) | Таможенный платеж (руб.) | Итого стоимость партии (руб.) | Цена за единицу (руб.) |
| 0,03 | 1000 | 29,31 | 29,45% | 258,95 | 1138,25 | 1,13825 |
Таблица 2.2. Пример правильного расчета таможенных платежей и стоимости товара
В Excel существует более 10 функций округления, каждая из которых выполняет эту операцию по-своему. Часть из них представлена на рис. 2.29. Исчерпывающую информацию относительно всех этих функций вы можете получить в справке Excel, вызываемой путем нажатия функциональной клавиши .
Рис. 2.29. Функции округления в Excel
Правила округления десятичной дроби
Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.
В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:
— Который час?
— Какой вес?
— Сколько стоит?
Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).
Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.
Число, полученное при округлении, называют приближенным значением данного числа.
Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.
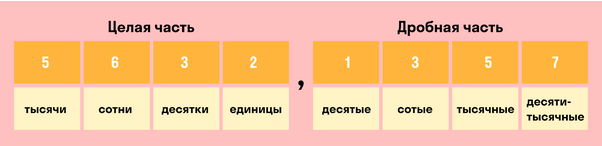
Если число c < х < d, тогда с — это приближенное значение x с недостатком. А d — это приближенное значение x с избытком.
Чтобы округлить дробную часть десятичной дроби, пользуйтесь следующими правилами:
- Подчеркните цифру округляемого разряда.
- Отделите все цифры, стоящие справа.
- Если справа от цифры, которую нужно округлить, стоит 0, 1, 2, 3 или 4 — цифра остается без изменений. Отбросьте все цифры справа от цифры округляемого разряда.
- Если справа от цифры округляемого разряда стоит 5, 6, 7, 8 или 9 — к цифре округляемого разряда прибавляем один. Отбросьте все цифры справа.
Приближенное значение записывается после вот такого знака: ≈
|
Еще одно правило округления, которое нужно запомнить Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число. Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел. |
Правила округления
Коммерческое округление
В Коммерческие туры (не отрицательные числа) выглядит следующим образом :
- Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
- Если число в первом десятичном разряде — 5, 6, 7, 8 или 9, то оно округляется в большую сторону.
Это правило округления описано в стандарте DIN 1333 . Округление часто уже преподается в начальной школе.
Примеры (округление до двух знаков после запятой):
- 13,3749 … € ≈ 13,37 €
- 13,3750 … € ≈ 13,38 €
Отрицательные числа в зависимости от их величины округлой формы, на 5 , чтобы сказать от нуля ( Engl : от нуля ):
- −13,3749 … € ≈ −13,37 €
- −13,3750 … € ≈ −13,38 €
В Коммерческих турах частично в правовой среде , как гражданские раунды , называемых и г. Б. в о поставщиках государственных услуг пояснил следующее:
Симметричное закругление
Коммерческое и симметричное округление отличаются друг от друга только тем, что число округляется точно посередине между двумя числами с выбранным количеством десятичных цифр.
Симметричные (или геодезическим, математический, искажаются, научный ) округление определяются следующим образом (композиция адаптирована):
- Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
- Если цифра 5 (за которой следуют другие цифры, которые не все равны нулю), 6, 7, 8 или 9 в первом десятичном разряде, она округляется в большую сторону.
- Если число в первом десятичном разряде — только 5 (или 5, за которой следуют только нули), оно округляется таким образом, чтобы последнее сохраняемое число было четным («правило четных чисел»).
Этот тип округления используется в числовой математике , инженерии и технике. Он предусмотрен стандартом IEEE 754 для вычислений с двоичными числами с плавающей запятой в компьютерах. В англоязычной литературе это называется Round to Even или Banker’s Rounding .
Примеры (округление до одного десятичного знака):
- 2,2499 ≈ 2,2 (по правилу 1)
- 2,2501 ≈ 2,3 (по правилу 2)
- 2,2500 ≈ 2,2 (округлено до четного числа согласно правилу 3)
- 2,3500 ≈ 2,4 (округлено до четного числа согласно правилу 3)
Коммерческое округление, описанное в предыдущем разделе, создает небольшие систематические ошибки, поскольку округление на 0,5 происходит в большую сторону, а в меньшую сторону на 0,5 никогда не происходит; это может немного исказить статистику. Описанное здесь математическое округление всегда округляется в большую или меньшую сторону от точной середины между двумя цифрами до следующей четной цифры. В результате среднее значение округляется в сторону увеличения и уменьшения примерно так же часто, по крайней мере, если исходные числа являются стохастическими . (Контрпример: если маленькие числа встречаются чаще, чем большие, их можно систематически округлять в меньшую сторону, а не в большую, см . Закон Бенфорда .)
Округление с сохранением суммы
При округлении с сохранением суммы слагаемые округляются таким образом, чтобы их сумма была равна округленной сумме слагаемых. Может потребоваться округлить некоторые слагаемые от ближайшего округленного значения до противоположного значения.
Важными приложениями являются пропорциональное распределение мест и распределение всего НДС в счете-фактуре по его отдельным позициям.
Случай, когда все слагаемые положительные, был тщательно исследован, см. Процедуру распределения мест .
Метод Хара-Нимейера может быть обобщен для слагаемых с обоими знаками : вы округляете все числа до ближайших круглых чисел, и пока сумма слишком велика (или слишком мала), вы выбираете одно из округленных (или округленных) чисел. ) нумерует с наибольшим округление (или самое большое количество округления вниз) и изменяет его округления в направлении , противоположном. Это означает, что сумма сумм изменений минимальна .
Округление в Excel в меньшую сторону с помощью функции ОКРУГЛВНИЗ
Эта функция работает аналогичным образом, как и предыдущая. Имеет те же самые аргументы и синтаксис, а также такие же особенности использования. Единственное отличие – округление осуществляется по направлению вниз (от большего числа к меньшему, проще говоря). Отсюда и название.
Все правила использования также аналогичные. Так, если второй аргумент (их приведем немного позже) равен нулю, о округляется число до целого. Если меньше 0, то сокращается количество разрядов перед запятой. Если же он больше нуля, то – после. Таким обрзаом можно убрать определенное количество десятичных дробей.
Синтаксис функции ОКРУГЛВНИЗ
Итак, синтаксис абсолютно аналогичный предыдущему примеру. Соответственно, нчем он особенно не отличается. Но если есть такое желание – Excel дает возможность самостоятельно использовать эту функции.
Для начала нужно зайти на нужный документ, открыть правильный лист и начать писать в строке ввода формулы знак равно. После этого необходиом непосредственно указать название формулы ОКРУГЛВНИЗ, после чего ввести два аргумента.
В общем, формула выглядит следующим образом.
=ОКРУГЛВНИЗ(3,2; 0)
А теперь более детально разберемся с тем, какие аргументы имеет эта функция.
Аргументы функции ОКРУГЛВНИЗ
В этом случае аргументы абсолютно те же, что и в предыдущем варианте. Сначала нужно указывать те числа, которые нужно округлить (одно число или целый диапазон), после чего через точку с запятой указать количество разрядов, которые будут сокращаться. Все остальные правила полностью аналогичны.
Таким образом, округление в Excel – очень простая, но полезная функция, которая дает возможность человеку значительно упрощать вычисления или восприятие. Главное – четко понимать, какой метод и в каких конкретно ситуациях должен использоваться. Если нам нужно лишь визуально отобразить данные (печать – это лишь одно из возможных применений), то нужно применять формат ячеек.
Если же человеку требуется выполнять полноценные математические операции, то тогда использование функции или формулы является единственным возможным вариантом. Правда, такие ситуации бывают довольно редко. Значительно чаще люди наоборот, мысленно окргуляют.
Неточные вычисления
Внутри JavaScript число представлено в виде 64-битного формата IEEE-754. Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 из них для хранения положения десятичной точки (если число целое, то хранится 0), и один бит отведён на хранение знака.
Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:
Наиболее часто встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.
Посмотрите на это (неверное!) сравнение:
Да-да, сумма и не равна .
Странно! Что тогда, если не ?
Но почему это происходит?
Число хранится в памяти в бинарной форме, как последовательность бит – единиц и нулей. Но дроби, такие как , , которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.
Другими словами, что такое ? Это единица делённая на десять — , одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: , которая становится бесконечной дробью .
Деление на гарантированно хорошо работает в десятичной системе, но деление на – нет. По той же причине и в двоичной системе счисления, деление на обязательно сработает, а становится бесконечной дробью.
В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.
Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.
Пример:
И когда мы суммируем 2 числа, их «неточности» тоже суммируются.
Вот почему – это не совсем .
Не только в JavaScript
Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.
Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):
Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она все равно появляется при финальном делении:
Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.
Забавный пример
Попробуйте выполнить его:
Причина та же – потеря точности. Из 64 бит, отведённых на число, сами цифры числа занимают до 52 бит, остальные 11 бит хранят позицию десятичной точки и один бит – знак. Так что если 52 бит не хватает на цифры, то при записи пропадут младшие разряды.
Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».
Два нуля
Другим забавным следствием внутреннего представления чисел является наличие двух нулей: и .
Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль.
В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.
32 Comments
Не правильная теория про если цифра 46.5 это не 47 а 46 это называется еще банковским округлением к ближайшему четному округляется если после запятой 5 и за ним нет никакой цифры
как округлить число 6,9?
Чтобы округлить число до целого, надо отбросить все числа, стоящие после запятой. Отбрасываем 9, поэтому предыдущее число следует увеличить на единицу. Значит, 6,9 приближенно равно семи целым.
На самом деле действительно не увеличивается цифра если после запятой 5 в любом финансовом учреждении
Гм. В таком случае финансовые учреждения в вопросах округления руководствуются не законами математики, а своими собственными соображениями.
Скажите, как округлить 46,466667. Запуталась
Если требуется округлить число до целого, то надо отбросить все цифры, стоящие после запятой. Первая из отброшенных цифр равна 4, поэтому предыдущую цифру не изменяем:
Уважаемая Светлана Ивановна. Плохо же Вы знакомы с правилами математики.
Правило. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т. е. последняя сохраняемая цифра оставляется неизменной, если она четная, и усиливается, если она нечетная.
И Соответственно: Округляя число 0,0465 до третьего десятичного знака, пишем 0,046. Усиления не делаем, так как последняя сохраняемая цифра 6 — четная. Число 0,046 столь же близко к данному, как 0,047.
Уважаемый гость! Да будет Вам известно, в математике для округление числа существуют различные способы округления. В школе изучают один из них, состоящий в отбрасывании младших разрядов числа. Я рада за Вас, что Вы знаете другой способ, но неплохо бы не забывать и школьные знания.
Спасибо вам большое! Нужно было округлить 349,92. Получается 350. Спасибо за правило
как правильно округлить 5499,8?
Если речь об округлении до целого, то отбросить все цифры, стоящие после запятой. Отброшенная цифра — 8, следовательно, предыдущую увеличиваем на единицу. Значит, 5499,8 приближенно равно 5500 целым.
Доброго дня! А вот такой вопрос возник сейас: Есть три числа: 60.56% 11.73% и 27.71% Каким образом окрулить до целых знаечний? Чтобы в сумме то 100 осталось. Если просто округлять, то 61+12+28=101 Плучается неувязочка. (Если, как тыт писали, по «банковскому» методу — в данном случае получится, но в случае, например 60.5% и 39.5% получится опять что-то пало — 1% потеряем). Как быть?
О! помог метод от «гость 02.07.2015 12:11″ Благодарю»
Не знаю меня в школе учили так: 1.5 => 1 1.6 => 2 1.51 => 2 1.51 => 1.6
Возможно, Вас так учили.
По моему у Вас ошибочка в последнем выражении. 1.5 => 1 1.6 => 2 1.51 => 2 «1.51 => 1.5»
0, 855 до сотых помогите пожалуйста
0, 855≈0,86 (отброшена 5, предыдущую цифру увеличиваем на 1).
Округлить 2,465 до целого числа
2,465≈2 (первая отброшенная цифра — 4. Поэтому предыдущую оставляем без изменения).
Как округлить 2,4456 до целого?
2,4456 ≈ 2 (так как первая отброшенная цифра 4, предыдущую цифру оставляем без изменения).
Исходя из правил кругления: 1,45=1,5=2, следовательно 1,45=2. 1,(4)5 = 2. Так ли это?
Нет. Если требуется округлить 1,45 до целого, отбрасываем первую цифру после запятой. Поскольку это 4, предыдущую цифру не изменяем. Таким образом, 1,45≈1.
А если мне нужно округлить 103, это будет 100 или 105? (нужно округлить до 0 или 5)
Ирина, 103 — это уже целое число. Округлять до целого его не нужно. Если требуется округлить 103 до десятков, тогда 103≈100.
Источник
Excel. Формулы. Округление до кратного
При работе с числовыми данными операции округления совсем не редки. Чаще всего мы подразумеваем под ними округление до некоторого числа разрядов (обычно — после запятой). Сюда же можно отнести и округление до десятков, сотен, тысяч и т.д.
Однако, иногда возникает необходимость округлить число с нужной точностью, то есть до ближайшего числа, кратного заданному. Например, 19 округлить с точностью до 5 (результат — 20, ближайшее к 19 число, которое кратно 5).
Для подобного рода округлений в Excel есть встроенная математическая функция ОКРУГЛТ(). Она принимает 2 аргумента:
- округляемое число (в примере выше — 19);
- точность округления (в примере выше — 5).
Данная функция производит округление с избытком, то есть делит исходное число на указанную точность, и если остаток от деления больше или равен половине точности, то возвращается первое число, которое больше исходного и кратно заданному. Иначе возвращается первое число, которое меньше исходного и кратно заданному. Пример вычисления — на рисунке ниже.
В качестве точности можно указывать и положительные, и отрицательные числа, и десятичные дроби. Единственное правило — знак исходного числа и числа, указывающего точность, должен быть одинаковым , иначе функция вернет ошибку #!ЧИСЛО.
Несколько примеров вычисления:
Если Вам нужно округлять число с кратностью 10, 100, 1000 и т.д., то можно использовать для этого другую функцию — ОКРУГЛ(). В качестве второго аргумента нужно указать отрицательное число, указывающее на количество разрядов, до которых нужно округлить. Так, чтобы округлить число 156 до десятков, нужно ввести формулу =ОКРУГЛ(156;-1) , а чтобы округлить число 123456 до 1000, ввести =ОКРУГЛ(123456;-3) .
Иногда нужно получить на выходе число, оканчивающееся, например, на 99 (как на ценниках в магазинах). В таком случае следует округлить заданное число кратно 100, а затем вычесть единицу. Формула будет выглядеть так: =ОКРУГЛТ(15678;100)-1 или =ОКРУГЛ(15678;-2)-1, а результат будет равен 15699.
Видеоверсию данной статьи смотрите на нашем канале на YouTube
Куча интересного по другим офисным приложениям от Microsoft (Word, Outlook, Power Point, Visio и т.д.) — на нашем канале в Telegram Office Killer
Вопросы по Excel можно задать нашему боту обратной связи в Telegram @ExEvFeedbackBot
Вопросы по другому ПО (кроме Excel) задавайте второму боту — @KillOfBot
Точные правила округления чисел
При округлении десятичных дробей недостаточно просто отбросить цифры после округляемого разряда. Убедиться в этом можно на таком примере. Если в магазине куплено 2 кг 150 г конфет, то говорят, что приобретено около 2 кг сладостей. Если же вес составляет 2 кг 850 г, то производят округление в большую сторону, то есть около 3 кг. То есть видно, что иногда округляемый разряд изменен. Когда и как это проделывают, смогут ответить точные правила:
- Если после округляемого разряда следует цифра 0, 1, 2, 3 или 4, то округляемый оставляют неизменным, а все последующие цифры отбрасываются.
- Если после округляемого разряда следует цифра 5, 6, 7, 8 или 9, то округляемый увеличивают на единицу, а все последующие цифры также отбрасываются.
К примеру, как правильно дробь 7,41 приблизить к единицам. Определяют цифру, которая следует за разрядом. В данном случае это 4. Следовательно, согласно правилу, число 7 оставляют неизменным, а цифры 4 и 1 отбрасывают. То есть получаем 7.
Если округляется дробь 7,62, то после единиц следует цифра 6. Согласно правилу, 7 необходимо увеличить на 1, а цифры 6 и 2 отбросить. То есть в результате получится 8.
Представленные примеры показывают, как округлить десятичные дроби до единиц.
Приближение до целых
Отмечено, что округлять до единиц можно точно так же, как и до целых. Принцип один и тот же. Остановимся подробнее на округлении десятичных дробей до определенного разряда в целой части дроби. Представим пример приближения 756,247 до десятков. В разряде десятых располагается цифра 5. После округляемого разряда следует цифра 6. Следовательно, по правилам необходимо выполнить следующие шаги:
- округление в большую сторону десятков на единицу,
- в разряде единиц цифру 6 заменяют нулем,
- цифры в дробной части числа отбрасываются,
- в результате получают 760.
Обратим внимание на некоторые значения, в которых процесс математического округления до целых по правилам не отображает объективную картину. Если взять дробь 8,499, то, преобразовывая его по правилу, получаем 8
Но по сути это не совсем так. Если поразрядно округлить до целых, то вначале получим 8,5, а затем отбрасываем 5 после запятой, и осуществляем округление в большую сторону.
Получаем 9, что, в принципе, не сосем точно. То есть в таких значениях погрешность существенна. Поэтому оцениваем задачу и, если ситуация позволяет, то лучше использовать значение 8,5.
Приближение до десятых
Как округлить до десятых, до сотых, до тысячных? Операция осуществляется по таким же правилам, как и до целых. Основная задача – правильно определить округляемый разряд и знак, который следует за ним.
К примеру, дробь 6,7864 при доведении:
- до десятых становится равной 6,8,
- до сотых – 6,79,
- если округлить до тысячных, то получают 6,786.
Обратите внимание! Незнание этих правил очень удачно используют маркетологи. В магазинах, наблюдая ценник с указанием числа 5,99, большинством покупателей воспринимается цена, равная 5
В действительности же цена товара практически 6.
Математика учимся округлять числа
Правила округления чисел до десятых
Использование функций округления
Иногда нужно поменять точность расчетов с числовыми данными не для всего файла, а лишь для определенной области ячеек. В этом случае лучшим решением будет использование встроенных функций для работы с округлением чисел, которых существует несколько видов. Вот самые удобные и наиболее популярные:
- ОКРУГЛ – округление до числа с указанным количеством знаков после запятой по правилам математики.
- ОКРУГЛВВЕРХ – округление до ближайшего большего значения (по модулю).
- ОКРУГЛВНИЗ – округление до ближайшего меньшего значения (по модулю).
- ОКРУГЛТ – округление числа с желаемой точностью.
- ОКРВВЕРХ – округление с избытком до ближайшего числа, которое кратно заданному значению точности.
- ОКРВНИЗ – округление с недостатком до числа ближайшего числа, которое кратно заданному значению точности.
- ОТБР – округление до целого числа путем отбрасывания цифр после запятой.
- ЧЁТН – округление до ближайшего четного числа.
- НЕЧЁТ – округление до ближайшего нечетного числа.
Обобщенная формула для первых трех функций выглядит так: ФУНКЦИЯ(;). Например, для округления числа 3,14159265 до двух знаков после запятой, нам понадобится следующая формула: =ОКРУГЛ(3,14159265;2).
Пишем ее в нужную ячейку, не забывая в начале поставить знак равно.

После набора формулы щелкаем клавишу Enter и получаем в результате число 3,14.

В формулах функций ОКРУГЛТ, ОКРВВЕРХ и ОКРВНИЗ в качестве второго аргумента указывается кратность округления. Например, если стоит задача округлить число 13 до ближайшего числа, делящегося на 5 без остатка, следует написать следующую формулу: =ОКРУГЛТ(13;5).
Результатом вычисления будет число 15.

Последние три функции (ОТБР, ЧЁТН и НЕЧЁТ) используют всего 1 аргумент – само число или ячейка. Первая из них просто вернет его целую часть, а вторая и третья – ближайшее четное или нечетное числа, соответственно.

Сами функции можно прописать как внутри ячейки, так и в верхней строке формул, которая находится справа от надписи fx.
После того, как вы начнете вводить название функции, программа выдаст подсказки, благодаря которым можно выбрать точное название и избежать возможных опечаток. Перед написанием формулы не забывайте ставить знак равно (“=”).

В дополнение ко всему, есть возможность вызвать функци через вкладку “Формулы”. Откройте ее и выберите “Математические”. Появится список всех функций, расположенных по алфавиту, поэтому для поиска округления (ОКРУГЛ) нужно идти в нижнюю часть списка.

После того, как мы выберем нужную функцию, откроется окно для ее настройки.

В строке “Число” пишем координаты ячейки, значение которой нужно округлить. Также, вместо того, чтобы писать адрес ячейки вручную, можно просто находясь курсором в строке “Число” щелкнуть левой кнопкой мыши по нужной ячейке.
Далее переходим к строке “Число разрядов” и здесь пишем число знаков после запятой. Допустим, в нашем случае, пусть это будет 2.

После того, как все заполнено, нажимаем “OK” и получаем результат в первой строке, куда была вставлена функция округления.

Чтобы применить расчеты к остальным строкам столбца, наводим мышью на нижний правый угол ячейки, содержащей формулу. Курсор поменяет свой вид на небольшой крестик. Теперь, зажав его левой кнопкой мыши тянем формулу на оставшиеся строки, по которым нужно произвести расчет, после чего отпускаем кнопку.

Итого
Чтобы писать числа с большим количеством нулей:
- Используйте краткую форму записи чисел – , с указанным количеством нулей. Например: это с 6-ю нулями .
- Отрицательное число после приводит к делению числа на 1 с указанным количеством нулей. Например: это ( миллионных).
Для других систем счисления:
- Можно записывать числа сразу в шестнадцатеричной (), восьмеричной () и бинарной () системах счисления
- преобразует строку в целое число в соответствии с указанной системой счисления: .
- представляет число в строковом виде в указанной системе счисления .
Для преобразования значений типа и в число:
Используйте parseInt/parseFloat для «мягкого» преобразования строки в число, данные функции по порядку считывают число из строки до тех пор пока не возникнет ошибка.
Для дробей:
- Используйте округления , , , или .
- Помните, что при работе с дробями происходит потеря точности.
Ещё больше математических функций:
Документация по объекту Math
Библиотека маленькая, но содержит всё самое важное