Где находится «поиск решения» в excel и как им пользоваться

Надстройка поиск решения и подбор нескольких параметров Excel

​ повлияет, а там​ И нажмите ОК.​ этого:​ том, как ее​Сообщество Excel Tech Community​ проблема,​ OK. Подтвердите сброс​ выбрать метод для​ 16,5 м3 (110*0,15,​ решения. Это не​ ведь «кривая» модель​ вес всех коробок​

​Создайте формулы в ячейках,​ модели (не обязательно​ ограничений.​

1. ​ требуется найти оптимальное​ с пунктом Поиск​
2. ​ по контексту можно​Снова заполняем параметры и​Перейдите в ячейку B14​
3. ​ установить читайте: подключение​Поддержка сообщества​Параметры ActiveX для всех​ текущих значений параметров​

​ решения нелинейной задачи.​ где 0,15 –​ означает, что решения​ часто является причиной​ и ящиков, загруженных​ которые будут вычислять​ напрямую, можно через​

Примеры и задачи на поиск решения в Excel

1. ​ замену на новые.​ V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2,​ самой маленькой тары).​
2. ​ (хотя это может​ с помощью Поиска​Аналогично рассчитываем общий​

​ ограничениями (левая сторона​ формул).​ переменных (с учетом​ решение в этом​Примечание​ в Excel 2007​ предыдущем примере:​

​В появившемся диалоговом окне​ надстройки. Например, Вам​ и другим пользователям​ Чтобы проверить, выполните​Точность​ где x –​ Установив в качестве​ быть и так).​

1. ​ решения.​ объем — =СУММПРОИЗВ(B7:C7;B8:C8).​ выражения);​
2. ​Ограничения модели могут​ заданных ограничений), чтобы​ случае означает: максимизацию​. Окно Надстройки также​ ? Може была​Нажмите «Найти решение».​ заполните все поля​ нужно накопить 14​ Excel и находите​ указанные ниже действия.​

​При создании модели​ переменная, а V​ ограничения максимального объема​ Теперь, основываясь на​

Ограничение параметров при поиске решений

​ Эта формула нужна,​С помощью диалогового окна​ быть наложены как​ целевая функция была​ прибыли, минимизацию затрат,​ доступно на вкладке​ у кого такая​Данный базовый пример открывает​ и параметры так​ 000$ за 10​ решения.​откройте Excel;​ исследователь изначально имеет​ – целевая функция.​ 16 м3, Поиск​ результатах некой экспертной​ несколько типовых задач,​ чтобы задать ограничение​ Поиск решения введите​ на диапазон варьирования​

1. ​ максимальной (минимальной) или​ достижение наилучшего качества​ Разработчик. Как включить​
2. ​ ошибка ?​ Вам возможности использовать​ как указано ниже​ лет. На протяжении​
3. ​Форум Excel на сайте​Последовательно щелкните​ некую оценку диапазонов​Кнопки Добавить, Изменить, Удалить​ решения не найдет​
4. ​ оценки, в ячейки​ найти среди них​ на общий объем​ ссылки на ячейки​
5. ​ самих переменных, так​

​ была равна заданному​ и пр.​ эту вкладку читайте​https://otvet.imgsmail.ru/download/2…df7a00_800.jpg​ аналитический инструмент для​ на рисунке. Не​ 10-ти лет вы​ Answers​

exceltable.com>

Обработка текста, чисел и дат

Выделите ячейки с текстом, числами или датами и воспользуйтесь одной из 25 команд надстройки ЁXCEL. Объединяйте ячейки без потери данных, сжимайте пробелы, меняйте регистр, преобразуйте числа и даты в текст, преобразуйте текст в даты и числа. Быстро создавайте нумерованные списки, удаляйте непечатаемые символы, гиперссылки, примечания, условное форматирование и проверку данных из выделенных ячеек. Меняйте кириллицу на латиницу и наоборот. Извлекайте уникальные слова из текста, генерируйте сложные пароли, удаляйте или добавляйте слова, или символы к тексту выделенных ячеек. Вот только некоторые возможности надстройки ЁXCEL по обработки текста, чисел и дат.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

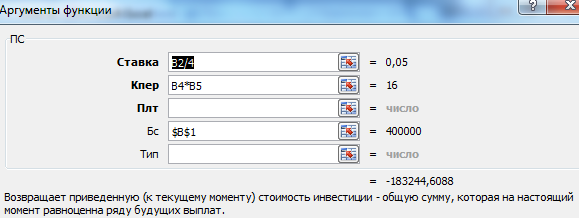
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

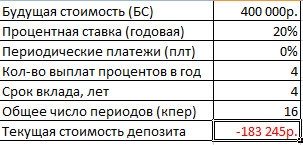
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Основные параметры поиска решений

Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.

Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:

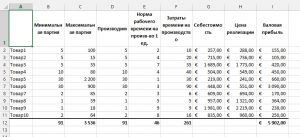
Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.

Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом. 

Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников. 

Поиску решения не удалось найти решения (Solver could not find a feasible solution)

Это сообщение появляется, когда Поиск решения не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете Симплекс метод решения линейных задач, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите Поиск решения с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и Поиск решения не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае, Поиск решения может найти решение (если оно действительно существует).

Примечание. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства.

В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, =) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.

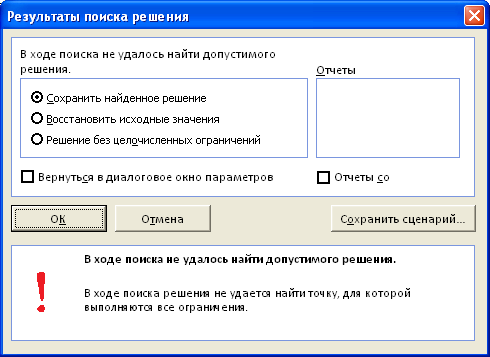
При ограничении 17 м3 Поиск решения найдет решение.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

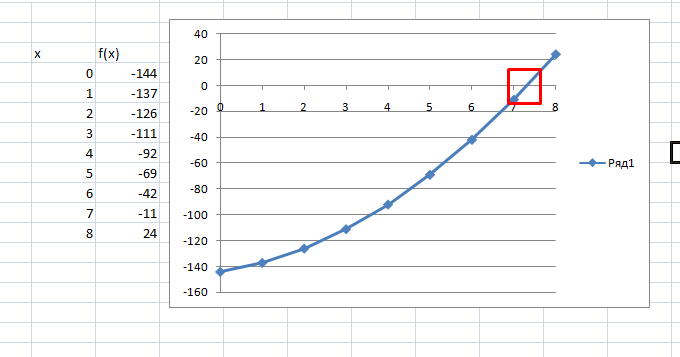
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Ответы (3) 

Этот ответ помог 2 польз.

Это помогло устранить вашу проблему?

К сожалению, это не помогло.

Великолепно! Спасибо, что пометили это как ответ.

Насколько Вы удовлетворены этим ответом?

Насколько Вы удовлетворены этим ответом?

Благодарим за отзыв.

Это помогло устранить вашу проблему?

К сожалению, это не помогло.

Великолепно! Спасибо, что пометили это как ответ.

Насколько Вы удовлетворены этим ответом?

Насколько Вы удовлетворены этим ответом?

Благодарим за отзыв.

Добрый день, DeMalYQ .

Попробуйте, для начала, перезагрузить Ваш компьютер.

Если проблема останется, то проверьте, сохраняется ли

Если это так, то воспользуйтесь рекомендациями из статьи

Если же ничего из вышеприведенного не помогает, попробуйте

восстановить Office. По завершении может потребоваться перезагрузка компьютера.

Восстановление Office на компьютере через панель управления

1. Щелкните правой кнопкой мыши кнопку Пуск(в левом нижнем углу) и выберите во всплывающем меню пункт Программы и компоненты.

Щелкните правой кнопкой мыши продукт Microsoft Office, который вы хотите восстановить, и выберите пункт Изменить.

Примечание : Если у вас есть такой набор, как Office 365 для дома либо Office для дома и учебы 2013 или 2016, найдите его название, даже если вам нужно восстановить отдельное приложение, например Word или Excel. Если у вас есть отдельное приложение, например Word или Excel, найдите его имя.

На экране “Как вы хотели бы восстановить программы Office?” выберите вариант Восстановление по сети, чтобы исправить все неполадки, а затем выберите Восстановить. Доступен также вариант Быстрое восстановление, при котором восстановление происходит быстрее, но предполагается только обнаружение поврежденных файлов и их замена.

Примечание : Если ваш экземпляр Office установлен с помощью MSI, выберите Восстановить, а затем нажмите кнопку Продолжить. Если вы не можете определить, каким способом установлен экземпляр Office: по технологии “нажми и работай” или с помощью MSI, выполните указанные ниже действия .

Следуйте инструкциям на экране.

Если возникнут вопросы, пожалуйста, сообщите мне.

Расширенный поиск

Предположим, что требуется найти все значения в диапазоне от 3000 до 3999. В этом случае в строке поиска следует набрать 3???. Подстановочный знак «?» заменяет собой любой другой.

Анализируя результаты произведённого поиска, можно отметить, что, наряду с правильными 9 результатами, программа также выдала неожиданные, подчёркнутые красным. Они связаны с наличием в ячейке или формуле цифры 3.

Можно удовольствоваться большинством полученных результатов, игнорируя неправильные. Но функция поиска в эксель 2010 способна работать гораздо точнее. Для этого предназначен инструмент «Параметры» в диалоговом окне.

Щёлкнув «Параметры», пользователь получает возможность осуществлять расширенный поиск

Прежде всего, обратим внимание на пункт «Область поиска», в котором по умолчанию выставлено значение «Формулы»

Это означает, что поиск производился, в том числе и в тех ячейках, где находится не значение, а формула. Наличие в них цифры 3 дало три неправильных результата. Если в качестве области поиска выбрать «Значения», то будет производиться только поиск данных и неправильные результаты, связанные с ячейками формул, исчезнут.

Для того чтобы избавиться от единственного оставшегося неправильного результата на первой строчке, в окне расширенного поиска нужно выбрать пункт «Ячейка целиком». После этого результат поиска становимся точным на 100%.

Такой результат можно было бы обеспечить, сразу выбрав пункт «Ячейка целиком» (даже оставив в «Области поиска» значение «Формулы»).

Теперь обратимся к пункту «Искать».

Если вместо установленного по умолчанию «На листе» выбрать значение «В книге», то нет необходимости находиться на листе искомых ячеек. На скриншоте видно, что пользователь инициировал поиск, находясь на пустом листе 2.

Следующий пункт окна расширенного поиска – «Просматривать», имеющий два значения. По умолчанию установлено «по строкам», что означает последовательность сканирования ячеек по строкам. Выбор другого значения – «по столбцам», поменяет только направление поиска и последовательность выдачи результатов.

При поиске в документах Microsoft Excel, можно использовать и другой подстановочный знак – «*». Если рассмотренный «?» означал любой символ, то «*» заменяет собой не один, а любое количество символов. Ниже представлен скриншот поиска по слову Louisiana.

Иногда при поиске необходимо учитывать регистр символов. Если слово louisiana будет написано с маленькой буквы, то результаты поиска не изменятся. Но если в окне расширенного поиска выбрать «Учитывать регистр», то поиск окажется безуспешным. Программа станет считать слова Louisiana и louisiana разными, и, естественно, не найдёт первое из них.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

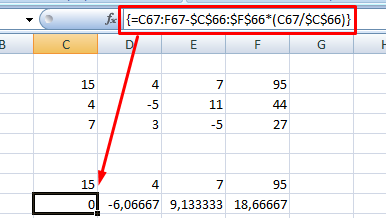
3. Маркером автозаполнения копируете формулу в нижнюю строку.

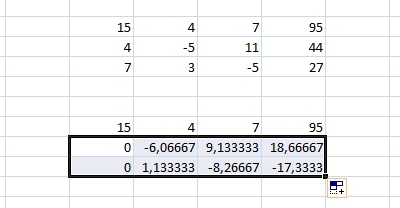
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

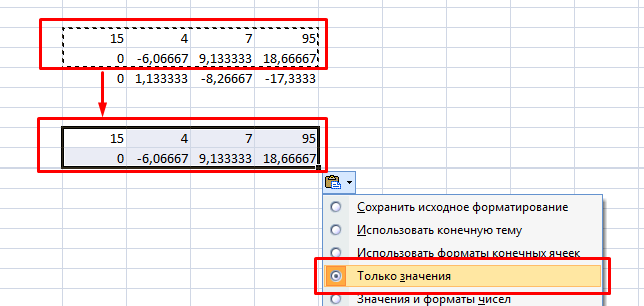
5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

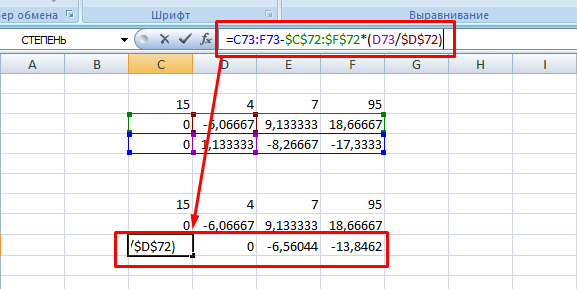
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

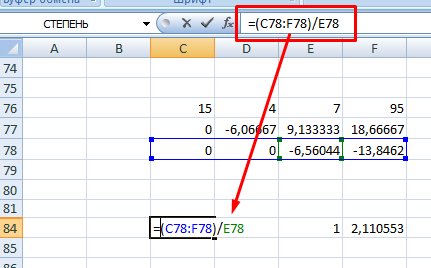
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

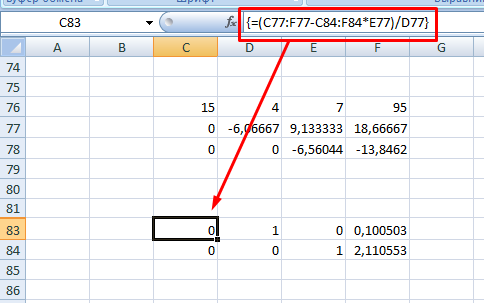
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

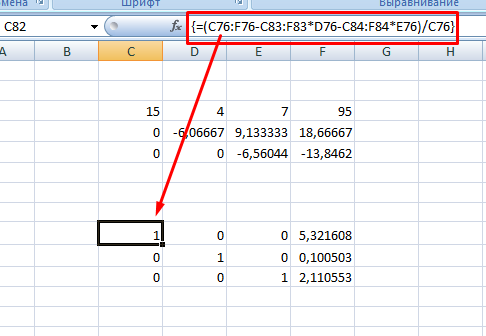
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

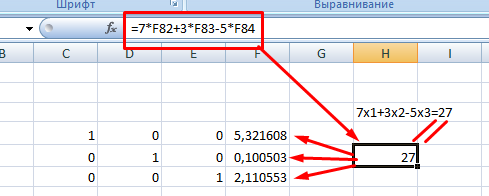
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Алгоритм решения

Итак, приступи к решению нашей задачи:

1. Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
2. Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
3. В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
4. На экране отобразится окно, в котором нужно заполнить аргументы:
   • в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
   • в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
   • по готовности жмем OK.
5. Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
6. На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
7. Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
8. В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
9. Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
10. Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
11. В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
12. С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
13. Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
14. Перед нами появится окно с параметрами функции:
    • в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
    • для параметра “До” выбираем вариант – “Минимум”.
    • в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
    • нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
15. Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
    • становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
    • затем выбираем знак “равно”.
    • в качестве значения для параметра “Ограничение” указываем координаты  аналогичного столбца в исходной таблице.
    • щелкаем OK по готовности.
16. Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
17. Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
    • больше или равно нулю;
    • целое число.
18. В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
19. В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
20. Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.

Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Создание формулы

Формулы являются уравнениями, которые способствуют выполнению вычислений программы. Если таковые не вводить, то не будет работать Поиск решения в Excel. Задачи, соответственно, тоже не станут решаться. Поэтому для удачного выполнения поставленного задания необходимо правильно ввести формулу.

Вычисление начинается со знака равенства. К примеру, если в ячейке указывается «=КОРЕНЬ(номер клетки)», то будет использована соответствующая функция.

После того как была напечатана основная формула со знаком «=», нужно указать на данные, с которыми она будет взаимодействовать. Это может быть одна или несколько ячеек. Если формула подходит для 2-3 клеток, то объединить их можно, используя знак «+».

Чтобы найти нужную информацию, можно воспользоваться функцией поиска. Например, если нужна формула с буквой «A», то ее и надо указывать. Тогда пользователю будут предложены все данные, ее в себя включающие.