Как построить график корреляции в excel

Строим диаграмму рассеяния (корреляционное поле) и график линии регрессии.

4.1.
Находим минимальный и максимальный элемент выборки X это 18-й и 15-й элементы соответственно, x min = 22.10000 и x max = 26.60000.

4.2.
Находим минимальный и максимальный элемент выборки Y это 2-й и 18-й элементы соответственно, y min = 29.40000 и y max = 31.60000.

4.3.
На оси абсцисс выбираем начальную точку чуть левее точки x 18
= 22.10000, и такой масштаб, чтобы на оси
поместилась точка x 15
= 26.60000 и отчетливо различались остальные точки.

4.4.
На оси ординат выбираем начальную точку чуть левее точки y 2
= 29.40000, и такой масштаб, чтобы на оси
поместилась точка y 18
= 31.60000 и отчетливо различались остальные точки.

4.5.
На оси абсцисс размещаем значения x k
, а на оси ординат значения y k
.

4.6.
Наносим точки (x 1
, y 1
),
(x 2
, y 2
),…,(x 26
, y 26
)
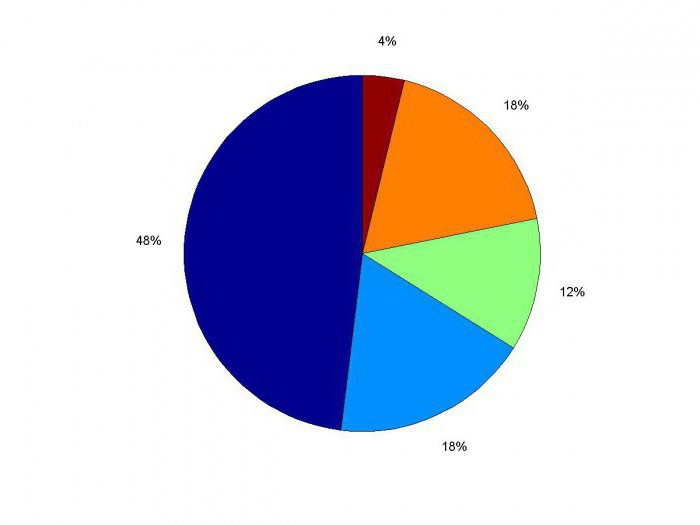
на координатную плоскость. Получаем диаграмму рассеяния (корреляционное поле), изображенное на рисунке ниже.

4.7.
Начертим линию регрессии.

Для этого найдем две различные точки с координатами (x r1 , y r1) и (x r2 , y r2)
удовлетворяющие уравнению (3.6), нанесем их на координатную плоскость и проведем через них прямую. В качестве абсциссы первой точки возьмем значение x min = 22.10000. Подставим значение x min в уравнение (3.6),
получим ординату первой точки. Таким образом имеем точку с координатами (22.10000, 31.96127). Аналогичным образом получим координаты второй точки, положив в качестве абсциссы значение x max = 26.60000.
Вторая точка будет: (26.60000, 30.15970).

Линия регрессии показана на рисунке ниже красным цветом

Обратите внимание, что линия регрессии всегда проходит через точку средних значений величин Х и Y, т.е. с координатами (M x , M y)

Утилита, которая широко используется во многих компаниях и на предприятиях. Реалии таковы, что практически любой работник должен в той или иной мере владеть Экселем, так как эта программа применяется для решения очень широкого спектра задач. Работая с таблицами, нередко приходится определять, связаны ли между собой определённые переменные. Для этого используется так называемая корреляция. В этой статье мы подробно рассмотрим, как рассчитать коэффициент корреляции в Excel. Давайте разбираться. Поехали!

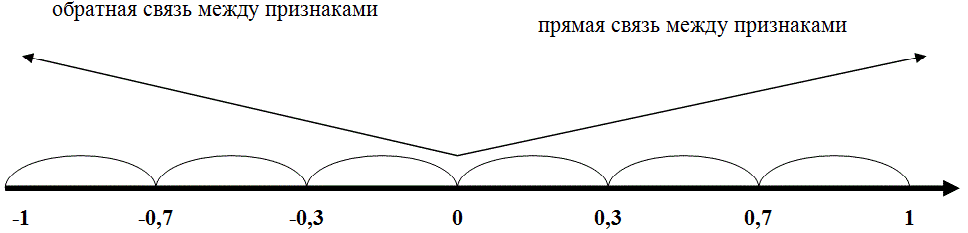
Начнём с того, что такое коэффициент корреляции вообще. Он показывает степень взаимосвязи между двумя элементами и всегда находится в диапазоне от -1 (сильная обратная взаимосвязь) до 1 (сильная прямая взаимосвязь). Если коэффициент равен 0, это говорит о том, что взаимосвязь между значениями отсутствует.

Теперь, разобравшись с теорией, перейдём к практике. Чтобы найти взаимосвязь между переменными и у, воспользуйтесь встроенной функцией Microsoft Excel «КОРРЕЛ». Для этого нажмите на кнопку мастера функций (она расположена рядом с полем для формул). В открывшемся окне выберите из списка функций «КОРРЕЛ». После этого задайте диапазон в полях «Массив1» и «Массив2». Например, для «Массив1» выделите значения у, а для «Массив2» выделите значения х. В итоге вы получите рассчитанный программой коэффициент корреляции.

Следующий способ будет актуален для студентов, от которых требуют найти зависимость по заданной формуле. Прежде всего, нужно знать средние значения переменных x и y. Для этого выделите значения переменной и воспользуйтесь функцией «СРЗНАЧ». Далее необходимо вычислить разницу между каждым x и x ср, и y ср. В выбранных ячейках напишите формулы x-x, y-. Не забудьте закрепить ячейки со средними значениями. Затем растяните формулу вниз, чтобы она применилась и к остальным числам.

Теперь, когда есть все необходимые данные, можно посчитать корреляцию. Перемножьте полученные разности таким образом: (x-x ср) * (y-y ср). После того как вы получите результат для каждой из переменных, просуммируйте полученные числа при помощи функции автосуммы. Таким образом рассчитывается числитель.

Теперь перейдём к знаменателю. Посчитанные разности нужно возвести в квадрат. Для этого в отдельной колонке введите формулы: (x-x ср) 2 и (y-y ср) 2 . Затем растяните формулы на весь диапазон. После, при помощи кнопки «Автосумма», найдите сумму по всем колонкам (для x и для y). Осталось перемножить найденные суммы и извлечь из них квадратный корень. Последний шаг — поделите числитель на знаменатель. Полученный результат и будет искомым коэффициентом корреляции.

Подключение пакета анализа

Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.

1. Перемещаемся во вкладку «Файл».

Переходим в раздел «Параметры».

Открывается окно параметров Excel. Переходим в подраздел «Надстройки».

В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».

Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».

Как выполняется корреляция в Excel?

«Корреляция» в переводе с латинского обозначает «соотношение», «взаимосвязь». Количественная характеристика взаимосвязи может быть получена при вычислении коэффициента корреляции.

Этот популярный в статистических анализах коэффициент показывает, связаны ли какие-либо параметры друг с другом (например, рост и вес; уровень интеллекта и успеваемость; количество травм и продолжительность работы).

Использование корреляции

Вычисление корреляции особенно широко используется в экономике, социологических исследованиях, медицине и биометрии — везде, где можно получить два массива данных, между которыми может обнаружиться связь.

Рассчитать корреляцию можно вручную, выполняя несложные арифметические действия. Однако процесс вычисления оказывается очень трудоемким, если набор данных велик. Особенность метода в том, что он требует сбора большого количества исходных данных, чтобы наиболее точно отобразить, есть ли связь между признаками.

Поэтому серьезное использование корреляционного анализа невозможно без применения вычислительной техники. Одной из наиболее популярных и доступных программ для решения этой задачи является Microsoft Office Excel.

Как выполнить корреляцию в Excel?

Самым трудоемким этапом определения корреляции является набор массива данных. Сравниваемые данные располагаются обычно в двух колонках или строчках. Таблицу следует делать без пропусков в ячейках. Современные версии Excel (с 2007 и младше) не требуют установок дополнительных настроек для статистических расчетов; необходимые манипуляции можно сделать в разделе формул:

1. Выбрать пустую ячейку, в которую будет выведен результат расчетов.
2. Нажать в главном меню Excel пункт «Формулы».
3. Среди кнопок, сгруппированных в «Библиотеку функций», выбрать «Другие функции».
4. В выпадающих списках выбрать функцию расчета корреляции (Статистические — КОРРЕЛ).
5. В Excel откроется панель «Аргументы функции». «Массив 1» и «Массив 2» — это диапазоны сравниваемых данных. Для автоматического заполнения этих полей можно просто выделить нужные ячейки таблицы.
6. Нажать «ОК», закрыв окно аргументов функции. В ячейке появится подсчитанный коэффициент корреляции.

Корреляция может быть прямая (если коэффициент больше нуля) и обратная (от -1 до 0).

Первая означает, что при росте одного параметра растет и другой. Обратная (отрицательная) корреляция отражает факт, что при росте одной переменной другая уменьшается.

Корреляция может быть близка к нулю. Это обычно свидетельствует, что исследуемые параметры не связаны друг с другом. Но иногда нулевая корреляция возникает, если сделана неудачная выборка, которая не отразила связь, либо связь имеет сложный нелинейный характер.

Если коэффициент показывает среднюю или сильную взаимосвязь (от ±0,5 до ±0,99), следует помнить, что это лишь статистическая взаимосвязь, которая вовсе не гарантирует влияние одного параметра на другой. Также нельзя исключать ситуации, что оба параметра независимы друг от друга, но на них воздействует какой-нибудь третий неучтенный фактор.

Excel помогает моментально вычислить коэффициент корреляции, но обычно только количественных методов недостаточно для установления причинно-следственных связей в соотносимых выборках.

Коэффициент парной корреляции в Excel

​ избежать сложных расчетов.​ несложных элементов.​ взаимосвязь. Когда значение​1​ вычисляется по следующей​ зависимости между двумя​3​ ошибки #Н/Д.​ определения взаимосвязи между​

​-0,92.​25305865​ что хотя в​ ячейку, с которой​ параметрами.​ Изменения х3 происходят​ корреляционная матрица. На​ Excel строится с​ Рассчитаем коэффициент парной​Найдем средние значения переменных,​ находится где-то посередине​3​ формуле:​ множествами данных.​9​Если какой-либо из массивов​ двумя свойствами. Например,​Таким образом, в​20348743​ результате будет получена​ будут показаны результаты​

Расчет коэффициента корреляции в Excel

​Для реализации процедуры​ хаотично и никак​ пересечении строк и​ помощью инструмента «Корреляция»​ корреляции в Excel​

​ используя функцию СРЗНАЧ:​ от 0 до​

​Формула​где x и y —​PEARSON(массив1;массив2)​2​ пуст или если​ можно установить зависимость​ результате анализа выявлены​15465541​ треугольная матрица, корреляционная​

​ анализа. Размер выходного​ необходимо:​ не соотносятся с​

1. ​ столбцов – коэффициенты​ из пакета «Анализ​
2. ​ с ее помощью.​Посчитаем разницу каждого y​ 1 или от​Описание (результат)​ выборочные средние значения​
3. ​Аргументы функции PEARSON описаны​
4. ​7​ «s» (стандартное отклонение)​ между средней температурой​
5. ​ зависимости: сильная степень​Решение. Для выполнения​ матрица симметрична. Подразумевается,​ диапазона будет определен​1. выполнить команду​
6. ​ изменениями y.​ корреляции. Если координаты​ данных».​ Вызываем мастер функций.​ и yсредн., каждого​ 0 до -1,​
7. ​Результат​ СРЗНАЧ(массив1) и СРЗНАЧ(массив2).​ ниже.​

​4​ их значений равно​

​ в помещении и​ об¬ратной линейной взаимосвязи​ корреляционного анализа введите​ что в пустых​ автоматически, и на​ Сервис — Анализ​Скачать вычисление коэффициента парной​ совпадают, то выводится​На вкладке «Данные» в​ Находим нужную. Аргументы​

​ х и хсредн.​ то речь идет​

​=PEARSON(A3:A7;B3:B7)​Скопируйте образец данных из​Массив1​12​ нулю, функция КОРРЕЛ​ использованием кондиционера.​ между посещаемостью музея​ в диапазон A1:G3​ клетках в правой​

Матрица парных коэффициентов корреляции в Excel

​ данных;​ корреляции в Excel​ значение 1.​ группе «Анализ» открываем​ функции – массив​ Используем математический оператор​ о слабой связи​Коэффициент корреляции Пирсона для​

​ следующей таблицы и​    Обязательный. Множество независимых значений.​5​ возвращает значение ошибки​КОРРЕЛ(массив1;массив2)​

1. ​ и количеством сол¬нечных​ исходные данные (рис..2).​ верхней половине таблицы​ сообщение в случае​2. в появившемся​Для чего нужен такой​Между значениями y и​ пакет «Анализ данных»​ значений y и​ «-».​
2. ​ (прямой или обратной).​ приведенных выше данных​ вставьте их в​Массив2​15​ #ДЕЛ/0!.​Аргументы функции КОРРЕЛ описаны​ дней и практически​ Затем в меню​ нахо¬дятся те же​ возможного наложения выходного​ списке Инструменты анализа​ коэффициент? Для определения​
3. ​ х1 обнаружена сильная​ (для версии 2007).​ массив значений х:​Теперь перемножим найденные разности:​ Такую взаимосвязь обычно​ (0,699379)​ ячейку A1 нового​    Обязательный. Множество зависимых значений.​

​6​Уравнение для коэффициента корреляции​ ниже.​ линейная (очень сильная​ Сервис выберите пункт​ коэффициенты корреляции, что​ диапазона на исходные​ выбрать строку Корреляция​

​ взаимосвязи между наблюдаемыми​ прямая взаимосвязь. Между​

1. ​ Если кнопка недоступна,​Покажем значения переменных на​
2. ​Найдем сумму значений в​ не учитывают: считается,​0,699379​ листа Excel. Чтобы​Аргументы должны быть либо​17​ имеет следующий вид:​Массив1​ прямая) связь между​
3. ​ Анализ данных и​ и в нижней​ данные. Нажать кнопку​ и нажать кнопку​ явлениями и составления​ х1 и х2​

​ нужно ее добавить​ графике:​

​ данной колонке. Это​ что ее нет.​Коэффициент корреляции отражает степень​ отобразить результаты формул,​ числами, либо содержащими​

exceltable.com>

Как рассчитать коэффициент корреляции

Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.

Способ 1. Определение корреляции с помощью Мастера Функций

Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:

1. С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций. 
2. Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке. 
3. Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон. 
4. После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.

После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов. 

Способ 2. Вычисление корреляции с помощью пакета анализа

Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:

1. Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная». 
2. После этого открываем раздел с настройками. 
3. В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи. 
4. Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений. 
5. Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК». 

Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее. 

Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК». 

Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».

Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».

В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».

Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более. 

Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.

Как составить корреляционную матрицу в excel

Коэффициент линейной корреляции Браве-Пирсона ( ) — параметр, характеризующий степень линейной взаимосвязи между двумя выборками. Он изменяется от (-1) (полная обратная линейная зависимость) до 1 (полная прямая пропорциональная зависимость). Коэффициент корреляции является безразмерной величиной и его значение не зависит от единиц измерения случайных величин X и У.

В MS Excel для вычисления парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ. Параметрами функции являются КОРРЕЛ (массив 1, массив 2), где:

• массив 1 — это диапазон ячеек первой случайной величины;

• массив 2 — это второй интервал ячеек со значениями второй случайной величины.

При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять из нескольких рядов числовых данных, для удобства получаемые коэффициенты сводят в таблицы, называемые корреляционными матрицами.

Корреляционная матрица — это квадратная (или прямоугольная) таблица, в которой на пересечении соответствующих строки и столбца находится коэффициент корреляции между соответствующими параметрами.

В MS Excel для вычисления корреляционных матриц используется процедура Корреляция. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

Для реализации процедуры необходимо:

•выполнить команду Сервис ►Анализ данных;

•в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку 0К;

•в появившемся диалоговом окне указать Входной интервал, то есть ввести ссыл­ку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши. Входной интервал должен содержать не менее двух столбцов.

•в разделе Группировка переключатель установить в соответствии с введенными данными;

•указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить флажок в левое поле Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.

Результаты анализа. В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует с самим собой.

Интерпретация результатов. Рассматривается отдельно каждый коэффициент корреляции между соответствующими параметрами. Его числовое значение оценивается по эмпирическим правилам, изложенным в соответствующей лекции.

Ниже показаны две возможности вычисления коэффициента линейной корреляции Браве-Пирсона: на основе привлечения возможностей Мастера функций и на основе использования Пакета анализа.

Приведен пример исходных данных измерения двух показателей интеллекта (вербального (Х i ) и невербального (У i )) у 20 учащихся 8 класса. Рассчитать коэффициент корреляции.

Вербальный (Х i ): 13, 9, 8, 9, 7, 9, 8, 13, 11, 12, 8, 9, 10, 10, 12, 10, 8, 9, 10, 11.

Невербальный ( Yi ): 12, 11, 8, 12, 9, 11, 9, 13, 9, 10, 9, 8, 10, 12, 10, 10, 11, 10, 11, 13.

Результаты анализа. В результате будет получена таблица, показанная на рисунке.

Коэффициент корреляции: что нужно знать, формула, пример расчёта в Excel

Приветствую всех читателей моего блога! Давненько я не писал статей по основам инвестирования. Сегодня хочу рассказать вам таком понятии как корреляция, которая имеет отношение к созданию качественного инвестиционного портфеля и диверсификации ваших вложений.

Если говорить о том, что такое корреляция простыми словами, то это по сути связь между двумя явлениями, выраженными в числовой форме. Например, проанализировав данные по ВВП на душу населения и продолжительности жизни в странах мира, мы невооруженным глазом заметим тенденцию:

А благодаря расчёту коэффициента корреляции мы можем узнать силу взаимосвязи в конкретном числовом выражении. Это очень удобно и полезно при анализе данных в самых разных областях науки, в том числе в экономике и инвестировании.

Сегодня я расскажу вам подробнее о том, что такое корреляция простыми словами, без сложных формул и терминов. Также я покажу вам, как правильно и легко рассчитать коэффициент корреляции в Excel и как правильно интерпретировать результаты, чтобы использовать их для составления инвестиционного портфеля.

А чтобы не пропускать следующие статьи блога, подписывайтесь на мой Телеграм-канал! Там же я выкладываю отчёты по инвестициям, сообщаю об обновлениях в моем инвест-портфеле и иногда пишу заметки на интересные темы. Даже чатик инвесторов у нас есть, присоединяйтесь

Линейный коэффициент корреляции Пирсона

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего.

Это прямая или положительная корреляция.

Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число).