Коэффициент корреляции

Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel

КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.

Примеры использования функции КОРРЕЛ в Excel

Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:

24

Алгоритм расчёта выглядит следующим образом:

25

Отображенный показатель близок к 1. Результат:

26

Определение коэффициента корреляции влияния действий на результат

Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.

27

Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:

• =КОРРЕЛ(А3:А17;В3:В17).
• =КОРРЕЛ(А3:А17;С3:С17).

Результаты:

28

Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.

Анализ популярности контента по корреляции просмотров и репостов видео

Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:

29

Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:

0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;”Сильная  прямая зависимость”;”Сильная обратная зависимость”);”Слабая зависимость или ее отсутствие”)’ class=’formula’>

Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:

30

Теперь производим построение графика:

31

Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:

32

Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);”Величины не взаимосвязаны”)’ class=’formula’>. Получаем следующие результаты:

33

Особенности использования функции КОРРЕЛ в Excel

Данная функция имеет нижеприведенные особенности:

1. Не учитываются ячейки пустого типа.
2. Не учитываются ячейки, в которых находится информация типа Boolean и Text.
3. Двойное отрицание «–» применяется для учёта логических величин в виде чисел.
4. Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.

Корреляция и диверсификация

Как знания о корреляции активов могут помочь лучше вкладывать деньги? Думаю, вы все хорошо знакомы с золотым правилом инвестора — не клади все яйца в одну корзину. Речь, естественно, идёт о диверсификации инвестиционных активов в портфеле. Корреляция и диверсификация неразрывно связаны, что понятно даже из названия — английское diversify означает «разнообразить», а как коэффициент корреляции как раз показывает схожесть или различие двух явлений.

Другими словами, инвестировать в финансовые инструменты с высокой корреляцией не очень хорошо. Почему? Все просто — похожие активы плохо диверсифицируются. Вот пример портфеля двух активов с корреляцией +1:

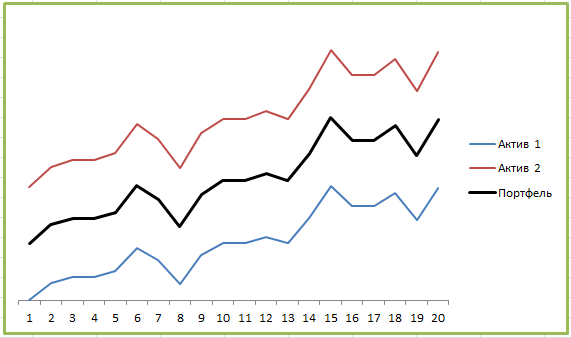
Как видите, график портфеля во всех деталях повторяет графики каждого из активов — рост и падение обоих активов синхронны. Диверсификация в теории должна снижать инвестиционные риски за счёт того, что убытки одного актива перекрываются за счёт прибыли другого, но здесь этого не происходит совершенно. Все показатели просто усредняются:

Портфель даёт небольшой выигрыш в снижении рисков — но только по сравнению с более доходным Активом 1. А так, никаких преимуществ по сути нет, нам лучше просто вложить все деньги в Актив 1 и не париться.

А вот пример портфеля двух активов с корреляцией близкой к 0:

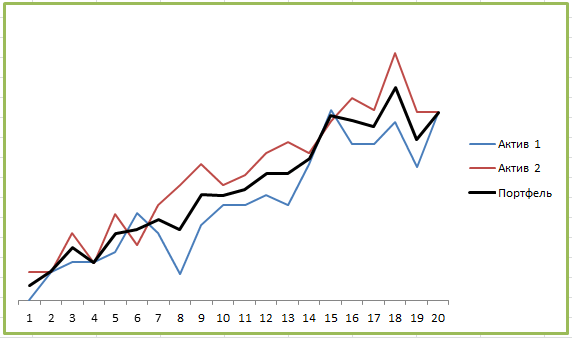
Где-то графики следуют друг за другом, где-то в противоположных направлениях, какой-либо однозначной связи не наблюдается. И вот здесь диверсификация уже работает:

Мы видим заметное снижение СКО, а значит портфель будет менее волатильным и более стабильно расти. Также видим небольшое снижение максимальной просадки, особенно если сравнивать с Активом 1. Инвестиционные инструменты без корреляции достаточно часто встречаются и из них имеет смысл составлять портфель.

Впрочем, это не предел. Наиболее эффективный инвестиционный портфель можно получить, используя активы с корреляцией -1:

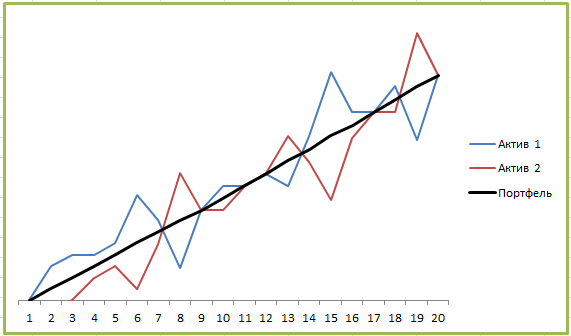
Уже знакомое вам «зеркало» позволяет довести показатели риска портфеля до минимальных:

Несмотря на то, что каждый из активов обладает определенным риском, портфель получился фактически безрисковым. Какая-то магия, не правда ли? Очень жаль, но на практике такого не бывает, иначе инвестирование было бы слишком лёгким занятием.

Регрессионный анализ в Excel

Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

Регрессия бывает:

• линейной (у = а + bx);
• параболической (y = a + bx + cx2);
• экспоненциальной (y = a * exp(bx));
• степенной (y = a*x^b);
• гиперболической (y = b/x + a);
• логарифмической (y = b * 1n(x) + a);
• показательной (y = a * b^x).

Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

У = а0 + а1х1 +…+акхк.

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

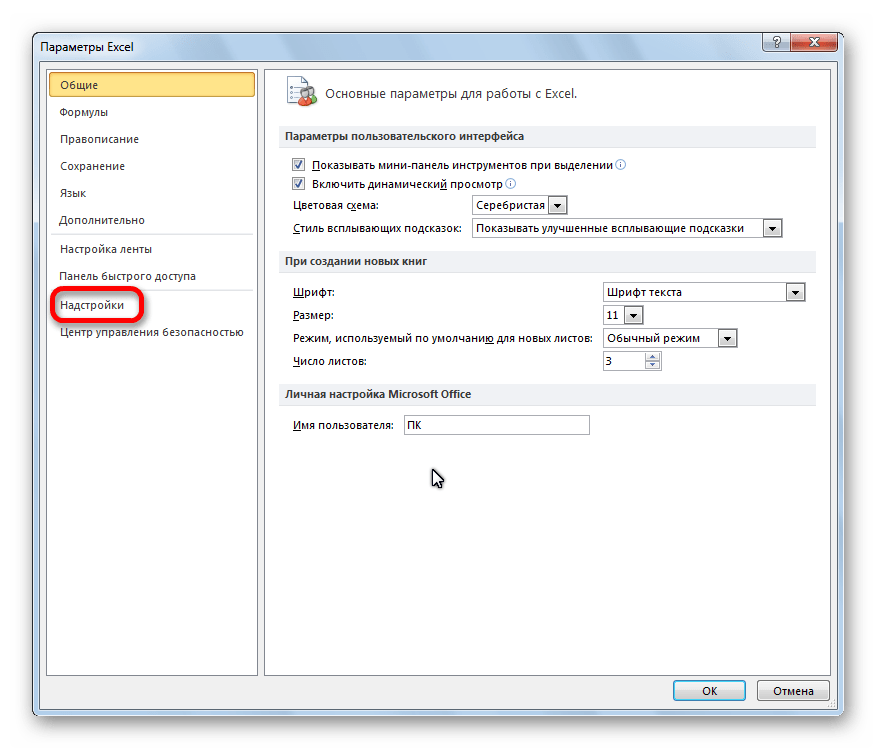
1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

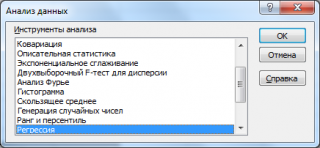
1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты. R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%

Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»

В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.

Коэффициент корреляции в Excel: что это, как рассчитать? Формула, пример, анализ данных онлайн

Выделяют 2 вида связи между ними:

• функциональная;
• корреляционная.

Корреляция в переводе на русский язык – не что иное, как связь. В случае корреляционной связи прослеживается соответствие нескольких значений одного признака нескольким значениям другого признака. В качестве примеров можно рассмотреть установленные корреляционные связи между:

• длиной лап, шеи, клюва у таких птиц как цапли, журавли, аисты;
• показателями температуры тела и частоты сердечных сокращений.

Для большинства медико-биологических процессов статистически доказано присутствие этого типа связи.

Статистические методы позволяют установить факт существования взаимозависимости признаков. Использование для этого специальных расчетов приводит к установлению коэффициентов корреляции (меры связанности).

Такие расчеты получили название корреляционного анализа. Он проводится для подтверждения зависимости друг от друга 2-х переменных (случайных величин), которая выражается коэффициентом корреляции.

Использование корреляционного метода позволяет решить несколько задач:

• выявить наличие взаимосвязи между анализируемыми параметрами;
• знание о наличии корреляционной связи позволяет решать проблемы прогнозирования. Так, существует реальная возможность предсказывать поведение параметра на основе анализа поведения другого коррелирующего параметра;
• проведение классификации на основе подбора независимых друг от друга признаков.

Для переменных величин:

• относящихся к порядковой шкале, рассчитывается коэффициент Спирмена;
• относящихся к интервальной шкале – коэффициент Пирсона.

Это наиболее часто используемые параметры, кроме них есть и другие.

Значение коэффициента может выражаться как положительным, так и отрицательными.

В первом случае при увеличении значения одной переменной наблюдается увеличение второй. При отрицательном коэффициенте – закономерность обратная.

Для чего нужен коэффициент корреляции?

Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.

Случайные величины, связанные между собой, могут иметь совершенно разную природу этой связи.

Не обязательно она будет функциональной, случай, когда прослеживается прямая зависимость между величинами.

9.1.2. Проверка статистических гипотез о связи переменных

Выборочный коэффициент корреляции оценивает подразумеваемую исследователем реальную связь между переменными. Как и в случае оценки среднего значения, нас интересуют два вопроса: (1) Насколько сильна связь между переменными; (2) Насколько надежна наша оценка. Сила связи между переменными по всей генеральной совокупности существует объективно. Если ее измерять корреляцией, то она будет выражаться числом от −1 до 1. Выборочная корреляция этих переменных будет колебаться вокруг истинного показателя силы связи. Трудность состоит в том, что, получив выборочную корреляцию, мы не можем знать, ни насколько она отклоняется от истинного значения, ни даже в какую сторону. В случае корреляции оценка обычно выражается в терминах значимости.

Проделаем небольшое упражнение.

Упражнение 9.1.2(1). Возьмите две симметричные монеты достоинством в один рубль и один евро. Проведите серию четырех подбрасываний пары монет и запишите результаты в виде ​\( (x_1, y_1),\dots,(x_4, y_4) \)​ , полагая

​\( x_i=0 \)​, если рубль выпал цифрой;

​\( x_i=1 \), если рубль выпал гербом;

​\( y_i=0 \), если евро выпал цифрой;

​\( y_i=1 \), если евро выпал гербом.

Подсчитайте коэффициент корреляции Пирсона. Истинная корреляция между результатами двух монет равна, разумеется, нулю. Повторите процедуру несколько раз и убедитесь, что нулевое значение выборочного коэффициента корреляции выпадает примерно один раз из трех. При многократном повторении опыта можно убедиться, что его результат имеет некоторое распределение, симметричное относительно нуля. Это распределение зависит от объема выборки n: чем больше n, тем меньше дисперсия распределения, тем ближе к нулю ее вероятные значения.

В таблице 9.1.2(2) приведены двухсторонние квантили распределения выборочного коэффициента корреляции по Пирсону для ​\( n=10 \)​. Они рассчитаны для выборок, полученных испытаниями двух нормально распределенных случайных величин, теоретическая корреляция между которыми равна нулю. Дихотомический результат подбрасывания монеты не распределен нормально, однако некоторое представление о возможных результатах наших испытаний табличный квантиль все же дает.

Таблица 9.1.2(2) Двусторонние квантили распределения коэффициента Пирсона для n = 10

​\( \alpha \)​	0.05	0.025	0.01	0.005
​\( r_\alpha(10) \)​	0.497	0.576	0.658	0.709

Обычно при исследовании связи переменных статистической гипотезой ​\( H_0 \)​ будет гипотеза об отсутствии связи, т.е. о независимости переменных. Альтернативная гипотеза \( H_1 \)​ (т.е. гипотеза, к которой мы склоняемся, получив большие по модулю значения выборочной корреляции) будет утверждать только наличие связи . Можно оценить значимость относительно данного результата (полученной парной выборки) гипотез о других значениях теоретической корреляции, но это требует некоторых дополнительных усилий (см. подпараграф ). Если истинна гипотеза \( H_0 \)​, то выборочный коэффициент корреляции будет принимать значения, более или менее близкие к нулю. Если выборочная корреляция принимает достаточно большое по модулю значение, которому соответствует значимость, измеряемая маленьким числом, то мы склоняемся к гипотезе \( H_1 \)​ о наличии связи, но без указания точного значения теоретической корреляции.

Можно заметить, что если верна гипотеза  об отсутствии зависимости между случайными величинами, то выборочный коэффициент при \( n=10 \) может принимать тем не менее довольно большие значения, так что уровень значимости 0.05 для принятия гипотезы о зависимости случайных величин требует, чтобы выборочный коэффициент корреляции достигал почти 0.5 (см. ). В связи с этим надо иметь в виду, что даже выборочная корреляция, например 0.6, вполне может согласовываться с истинной корреляцией, равной 0.2 .

Распространенные заблуждения

Корреляция и причинно-следственная связь

Традиционное изречение, что « корреляция не подразумевает причинно-следственную связь », означает, что корреляция не может использоваться сама по себе для вывода причинной связи между переменными. Это изречение не должно означать, что корреляции не могут указывать на возможное существование причинно-следственных связей. Однако причины, лежащие в основе корреляции, если таковые имеются, могут быть косвенными и неизвестными, а высокие корреляции также пересекаются с отношениями идентичности ( тавтологиями ), где не существует причинных процессов. Следовательно, корреляция между двумя переменными не является достаточным условием для установления причинно-следственной связи (в любом направлении).

Корреляция между возрастом и ростом у детей довольно прозрачна с точки зрения причинно-следственной связи, но корреляция между настроением и здоровьем людей менее очевидна. Приводит ли улучшение настроения к улучшению здоровья, или хорошее здоровье приводит к хорошему настроению, или и то, и другое? Или в основе обоих лежит какой-то другой фактор? Другими словами, корреляция может рассматриваться как свидетельство возможной причинной связи, но не может указывать на то, какой может быть причинная связь, если таковая имеется.

Простые линейные корреляции

Четыре набора данных с одинаковой корреляцией 0,816

Коэффициент корреляции Пирсона указывает на силу линейной связи между двумя переменными, но его значение, как правило, не полностью характеризует их взаимосвязь. В частности, если условное среднее из дано , обозначается , не является линейным в , коэффициент корреляции будет не в полной мере определить форму .
Y{\ displaystyle Y}Икс{\ displaystyle X}E⁡(Y∣Икс){\ displaystyle \ operatorname {E} (Y \ mid X)}Икс{\ displaystyle X}E⁡(Y∣Икс){\ displaystyle \ operatorname {E} (Y \ mid X)}

Прилегающие изображение показывает разброс участков из квартет энскомбы , набор из четырех различных пар переменных , созданный Фрэнсис Анскомбами . Четыре переменные имеют одинаковое среднее значение (7,5), дисперсию (4,12), корреляцию (0,816) и линию регрессии ( y  = 3 + 0,5 x ). Однако, как видно на графиках, распределение переменных сильно отличается. Первый (вверху слева), кажется, распределен нормально и соответствует тому, что можно было бы ожидать, рассматривая две коррелированные переменные и следуя предположению о нормальности. Второй (вверху справа) не распространяется нормально; хотя можно наблюдать очевидную взаимосвязь между двумя переменными, она не является линейной. В этом случае коэффициент корреляции Пирсона не указывает на то, что существует точная функциональная взаимосвязь: только степень, в которой эта взаимосвязь может быть аппроксимирована линейной зависимостью. В третьем случае (внизу слева) линейная зависимость идеальна, за исключением одного выброса, который оказывает достаточное влияние, чтобы снизить коэффициент корреляции с 1 до 0,816. Наконец, четвертый пример (внизу справа) показывает еще один пример, когда одного выброса достаточно для получения высокого коэффициента корреляции, даже если связь между двумя переменными не является линейной.
у{\ displaystyle y}

Эти примеры показывают, что коэффициент корреляции как сводная статистика не может заменить визуальный анализ данных. Иногда говорят, что примеры демонстрируют, что корреляция Пирсона предполагает, что данные следуют нормальному распределению , но это верно лишь отчасти. Корреляцию Пирсона можно точно рассчитать для любого распределения, имеющего конечную матрицу ковариаций , которая включает большинство распределений, встречающихся на практике. Однако коэффициент корреляции Пирсона (вместе с выборочным средним и дисперсией) является достаточной статистикой только в том случае, если данные взяты из многомерного нормального распределения. В результате коэффициент корреляции Пирсона полностью характеризует взаимосвязь между переменными тогда и только тогда, когда данные взяты из многомерного нормального распределения.

Виды коэффициента корреляции

Коэффициенты корреляции можно классифицировать по знаку и значению:

• положительный;
• нулевой;
• отрицательный.

В зависимости от анализируемых значений рассчитывается коэффициент:

• Пирсона;
• Спирмена;
• Кендала;
• знаков Фехнера;
• конкорддации или множественной ранговой корреляции.

Метод Пирсона рекомендуется использовать для ситуаций, требующих:

• точного установления корреляционной силы;
• сравнения количественных признаков.

Недостатков использования линейного корреляционного коэффициента Пирсона немного:

• метод неустойчив в случае выбросов числовых значений;
• с помощью этого метода возможно определение корреляционной силы только для линейной взаимосвязи, при других видах взаимных связей переменных следует использовать методы регрессионного анализа.

Ранговая корреляция определяется методом Спирмена, позволяющим статистически изучить связь между явлениями. Благодаря этому коэффициенту вычисляется фактически существующая степень параллелизма двух количественно выраженных рядов признаков, а также оценивается теснота, выявленной связи.

Метод Спирмена рекомендуется применять в ситуациях:

• не требующих точного определения значение корреляционной силы;
• сравниваемые показатели имеют как количественные, так и атрибутивные значения;
• равнения рядов признаков с открытыми вариантами значений.

Метод Спирмена относится к методам непараметрического анализа, поэтому нет необходимости проверять нормальность распределения признака. К тому же он позволяет сравнивать показатели, выраженные в разных шкалах. Например, сравнение значений количества эритроцитов в определенном объеме крови (непрерывная шкала) и экспертной оценки, выражаемой в баллах (порядковая шкала).

На эффективность метода отрицательно влияет большая разница между значениями, сравниваемых величин. Не эффективен метод и в случаях когда измеряемая величина характеризуется неравномерным распределением значений.

Генерирование джиттера

Поскольку каждое значение округлено до ближайшего сантиметра или килограмма, то значение, записанное как 180 см, на самом деле может быть каким угодно между 179.5 и 180.5 см, тогда как значение 80 кг на самом деле может быть каким угодно между 79.5 и 80.5 кг. Для создания случайных искажений, мы можем добавить случайные помехи в каждую точку данных роста в диапазоне между -0.5 и 0.5 и в том же самом диапазоне проделать с точками данных веса (разумеется, это нужно cделать до того, как мы возьмем логарифм значений веса):

График с джиттером выглядит следующим образом:

Как и в случае с внесением прозрачности в график рассеяния в первой серии постов об описательной статистике, генерирование джиттера — это механизм, который обеспечивает исключение несущественных факторов, таких как объем данных или артефакты округления, которые могут заслонить от нас возможность увидеть закономерности в данных.

Ссылки

Hardoon D., Szedmak S., Shawe-Taylor J. Canonical Correlation Analysis: An Overview with Application to Learning Methods // Neural Computation. — 2004. — Т. 16, вып. 12. — P. 2639–2664. — DOI:10.1162/0899766042321814. — PMID 15516276.
A note on the ordinal canonical-correlation analysis of two sets of ranking scores (Приведена программа на языке FORTRAN)- Journal of Quantitative Economics 7(2), 2009, pp. 173–199
Representation-Constrained Canonical Correlation Analysis: A Hybridization of Canonical Correlation and Principal Component Analyses (Приведена программа на языке FORTRAN)- Journal of Applied Economic Sciences 4(1), 2009, стр. 115–124

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии. Проверить статью на грамматические и орфографические ошибки.

Графическое представление коэффициента Фехнера

Пример №1. При разработке глинистого раствора с пониженной водоотдачей в высокотемпературных условиях проводили параллельное испытание двух рецептур, одна из которых содержала 2% КМЦ и 1% Na2CO3, а другая 2% КМЦ, 1% Na2CO3 и 0,1% бихромата калия. В результате получена следующие значения Х (водоотдача через 30 с).

X1	9	9	11	9	8	11	10	8	10
X2	10	11	10	12	11	12	12	10	9

Пример №2.
Коэффициент корреляции знаков, или коэффициент Фехнера, основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Вычисляется он следующим образом:

,

где n_a — число совпадений знаков отклонений индивидуальных величин от средней; n_b — число несовпадений.

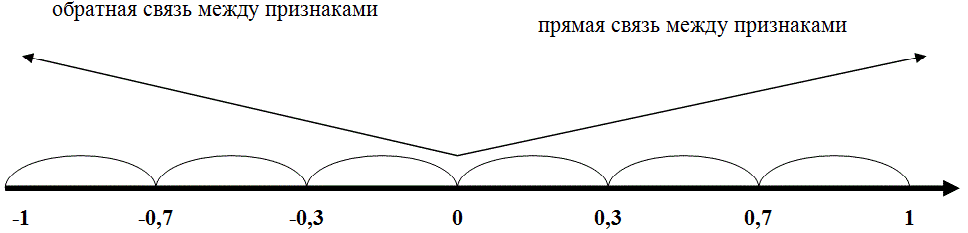
Коэффициент Фехнера может принимать значения от -1 до +1. Kф = 1 свидетельствует о возможном наличии прямой связи, Kф =-1 свидетельствует о возможном наличии обратной связи.

Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:

Xi	Yi	Знаки отклонений значений признака от средней	Совпадение (а) или несовпадение (в) знаков
Для Xi	Для Yi
8	40	—	—	А
9	50	—	+	В
10	48	—	+	В
10	52	—	+	В
11	41	+	—	В
13	30	+	—	В
15	35	+	—	В

Для примера: .

Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.

Пример №2
Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:
Средние значения:

Xi	Yi	Знаки отклонений от средней X	Знаки отклонений от средней Y	Совпадение (а) или несовпадение (b) знаков
12	220	+	—	B
9	1070	—	+	B
8	1000	—	+	B
14	606	+	—	B
15	780	+	+	A
10	790	—	+	B
10	900	—	+	B
15	544	+	—	B
93	5910

Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.

Интервальная оценка для коэффициента корреляции знаков

Пример №3.
Рассмотрим на примере расчет коэффициента корреляции знаков по данным, приведенным в таблице:

Xi	Yi	Знаки отклонений от средней X	Знаки отклонений от средней Y	Совпадение (а) или несовпадение (b) знаков
96	220	+	—	B
52	1070	—	+	B
60	1000	—	+	B
89	606	+	—	B
82	780	+	+	A
77	790	—	+	B
70	900	—	+	B
92	544	+	—	B
618	5910

Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.

Оценка коэффициента корреляции знаков. Значимость коэффициента корреляции знаков.
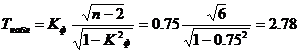По таблице Стьюдента находим t_табл:
t_табл (n-m-1;a) = (6;0.05) = 1.943
Поскольку Tнабл > tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции знаков. Другими словами, коэффициент корреляции знаков статистически — значим.

Доверительный интервал для коэффициента корреляции знаков.
Доверительный интервал для коэффициента корреляции знаков.
r(-1;-0.4495)

Проверяем значимость коэффициента корреляции (проверяем гипотезу зависимости).

Поскольку оценка коэффициента корреляции вычислена на конечной выборке, и поэтому может отклоняться от своего генерального значения,
необходимо проверить значимость коэффициента корреляции. Проверка производится с помощью t-критерия:

t =

Rx,y √ n — 2 √ 1 — R2x,y

( 2.1 )

Случайная величина t следует t-распределению Стьюдента
и по таблице t-распределения необходимо найти критическое значение критерия (t_кр.α) при заданном уровне
значимости α. Если вычисленное по формуле ( 2.1 ) t по модулю окажется меньше
чем t_кр.α, то зависимости между случайными величинами X и Y нет. В противном случае, экспериментальные
данные не противоречат гипотезе о зависимости случайных величин.
2.1.t

t =

-0.72028 √ 26 — 2 √ 1 — ( -0.72028)2

=  -5.08680

2.2.tt_кр.αt_кр.αα24α0.05t_кр.α2.064
Таблица 2    t-распределение

Число степеней свободы( n — 2 )	α = 0.1	α = 0.05	α = 0.02	α = 0.01	α = 0.002	α = 0.001
1	6.314	12.706	31.821	63.657	318.31	636.62
2	2.920	4.303	6.965	9.925	22.327	31.598
3	2.353	3.182	4.541	5.841	10.214	12.924
4	2.132	2.776	3.747	4.604	7.173	8.610
5	2.015	2.571	3.365	4.032	5.893	6.869
6	1.943	2.447	3.143	3.707	5.208	5.959
7	1.895	2.365	2.998	3.499	4.785	5.408
8	1.860	2.306	2.896	3.355	4.501	5.041
9	1.833	2.262	2.821	3.250	4.297	4.781
10	1.812	2.228	2.764	3.169	4.144	4.587
11	1.796	2.201	2.718	3.106	4.025	4.437
12	1.782	2.179	2.681	3.055	3.930	4.318
13	1.771	2.160	2.650	3.012	3.852	4.221
14	1.761	2.145	2.624	2.977	3.787	4.140
15	1.753	2.131	2.602	2.947	3.733	4.073
16	1.746	2.120	2.583	2.921	3.686	4.015
17	1.740	2.110	2.567	2.898	3.646	3.965
18	1.734	2.101	2.552	2.878	3.610	3.922
19	1.729	2.093	2.539	2.861	3.579	3.883
20	1.725	2.086	2.528	2.845	3.552	3.850
21	1.721	2.080	2.518	2.831	3.527	3.819
22	1.717	2.074	2.508	2.819	3.505	3.792
23	1.714	2.069	2.500	2.807	3.485	3.767
24	1.711	2.064	2.492	2.797	3.467	3.745
25	1.708	2.060	2.485	2.787	3.450	3.725
26	1.706	2.056	2.479	2.779	3.435	3.707
27	1.703	2.052	2.473	2.771	3.421	3.690
28	1.701	2.048	2.467	2.763	3.408	3.674
29	1.699	2.045	2.462	2.756	3.396	3.659
30	1.697	2.042	2.457	2.750	3.385	3.646
40	1.684	2.021	2.423	2.704	3.307	3.551
60	1.671	2.000	2.390	2.660	3.232	3.460
120	1.658	1.980	2.358	2.617	3.160	3.373
∞	1.645	1.960	2.326	2.576	3.090	3.291

2.2.tt_кр.αttt_кр.αэкспериментальные данные, с вероятностью 0.95αне противоречат гипотезе