Что такое синус (sin) — определение, график, свойства

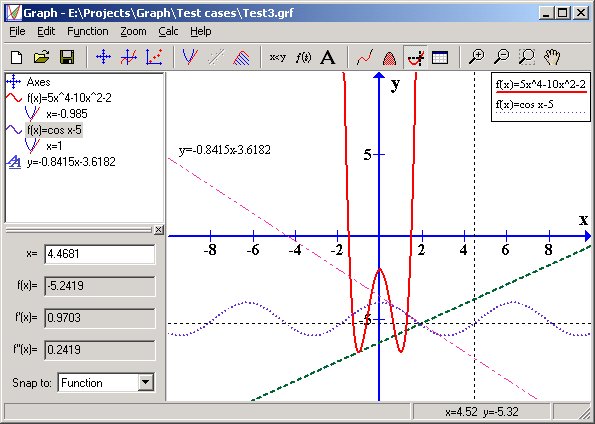
Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция  является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает:  или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:,  Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси  на  влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси  , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения:  – все действительные числа, кроме …  , , , … и т. д. или коротко: , где  – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция  не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси  к значению  справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси  к значению  слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

2.3.2. Синус и косинус window.top.document.title = «2.3.2. Синус и косинус»;

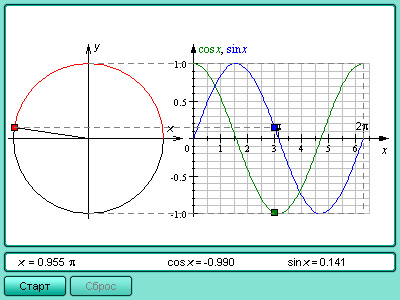
Положение точек на координатной окружности можно задавать не только длиной дуги, но и декартовыми координатами. Построим декартову систему координат с центром в точке O, осью абсцисс, проходящей через начало отсчета A (0), и осью ординат, проходящей через точку

За единицу отсчета возьмем радиус этой окружности. Декартовы координаты точки M (x) единичной окружности называются косинусом и синусом числа x:

Модель 2.9. Координатная окружность

Для

определение синуса и косинуса совпадает с геометрическим определением этих понятий, заданных при помощи прямоугольного треугольника OPM. В этом случае

Так как координаты точек окружности единичного радиуса по модулю не превосходят 1, то

Таким образом, областью значений обеих функций является отрезок .

Ниже приведены значения косинуса и синуса для некоторых значений x:

x 30° 45° 60° 90° 180° 270° sin x 1 –1 cos x 1 –1

Таблица 2.3.2.1

Функция sin x обращается в нуль при x = πn, функция cos x обращается в нуль при

График 2.3.2.1.Графики функций y = sin x и y = cos x.

in xcos x

Промежутки монотонности и знакопостоянства:

Функция sin x Неотрицателен, возрастает от 0 до 1 Неотрицателен, убывает от 1 до 0 Неположителен, убывает от 0 до –1 Неположителен, возрастает от –1 до 0 cos x Неотрицателен, убывает от 1 до 0 Неположителен, убывает от 0 до –1 Неположителен, возрастает от –1 до 0 Неотрицателен, возрастает от 0 до 1

Таблица 2.3.2.2

Синус достигает максимума в точках

и минимумы в точках

Косинус достигает максимума в точках x_max = 2πn, минимума – в точках x_min = π + 2πn.

Функция sin x нечетна, функция cos x четна:

Формулы приведения, позволяющие свести тригонометрические функции от любого аргумента к функциям от углов из промежутка

Основное тригонометрическое тождество (следствие теоремы Пифагора):

Некоторые тригонометрические формулы приведены в таблице.

График функции y = sin x называется синусоидой, а функции y = cos x – косинусоидой. В обоих случаях достаточно построить графики на отрезке или , а затем периодически продолжать их на всю ось. Более того, достаточно построить график y = sin x на отрезке

отразить симметрично относительно оси

а затем отразить получившийся график относительно точки (π; 0). График y = cos x после построения на отрезке

нужно отразить относительно точки

а затем получившийся график – относительно оси x = π. Заметим также, что косинусоида получается из синусоиды сдвигом на π/2 влево, поэтому, как правило, используется только термин «синусоида».

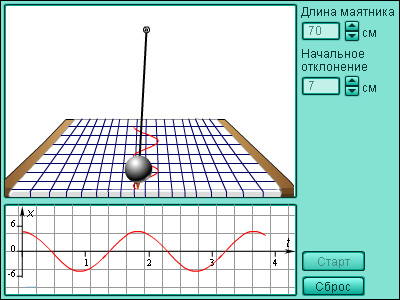
Модель 2.10. Математический маятник

Синус и косинус применяются во многих областях физики и математики. Например, с их помощью удобно описывать гармонические колебания, задаваемые формулами y = A cos (ωx + φ) или y = A sin (ωx + φ). Здесь A – амплитуда, ω – частота, φ – начальная фаза колебаний. Для построения графика гармонического колебания необходимо последовательно выполнить следующие операции над синусоидой:

• сжать к оси ординат с коэффициентом ω,
• перенести вдоль оси абсцисс на φ влево,
• растянуть от оси абсцисс в A раз.

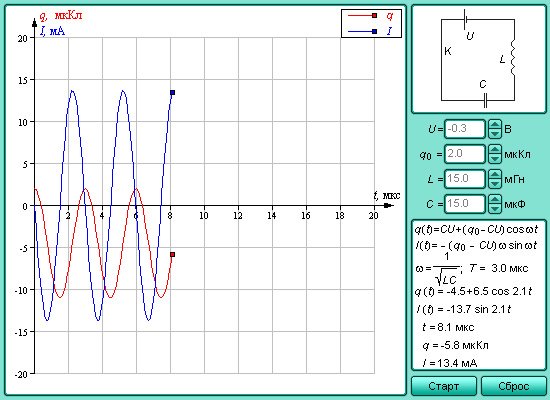
Если мы имеем дело с явлением, в котором одновременно происходят несколько различных колебательных процессов с соизмеримыми периодами, то зависимость колеблющейся величины от времени остается периодической, но график этой зависимости в общем случае уже не является синусоидой. Любую из функций, описывающих эту зависимость, можно представить в виде суммы постоянной составляющей и гармонических колебаний с частотами, кратными

Модель 2.11. Колебания в электрической цепи

Переменный (синусоидальный) ток и основные характеризующие его величины.

Переменный ток (англ. alternating current — AC) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.

В быту для электроснабжения переменяется переменный, синусоидальный ток.

Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):

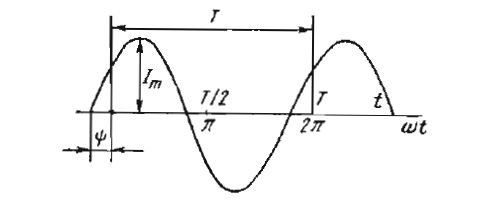
Рисунок 1

Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:

• амплитуду тока обозначают lm;
• амплитуду напряжения Um.

Период Т— это время, за которое совершается одно полное колебание.

Частота f равна числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с -1 )

f = 1/T

Угловая частота ω (омега) (единица угловой частоты — рад/с или с -1 )

ω = 2πf = 2π/T

Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.

Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)

В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.

Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).

Обратите внимание! При обозначении величин на схемах или в расчетах важен регистр букв, то есть заглавные буквы (E,I,U…) или строчные (e, i ,u…). Так как строчными буквами принято обозначать мгновенное значение, а заглавными могут обозначаться действующее значение величины (подробнее о действующем значении в следующей статье)

Источник

Синус против прямых

Не забывайте разделять идеи и примеры: квадрат — это лишь пример сочетания линий. А синус как понятие совсем не является «частью окружности».

Давайте рассмотрим синус в симуляторе.

Смайлик начнет свой путь:

• Нажмите start. Давай, смайлик, беги! Заметили это плавное движение вперёд-назад? Этот смайлик и есть синус. В таком же стиле вибрируют струны, сжимаются и разжимаются пружины, вращается маятник… и еще очень много разных тел движутся.
• Измените «vertical» на «linear». Большая разница — видите, какими резкими стали движения на краях амплитуды?

Давайте рассмотрим различия на видео:

https://youtube.com/watch?v=WAyTK6jF5o8

• Движение linear постоянно: мы движемся с постоянной скоростью и резко меняем направление. Это неестественное движение, как танцуют в стиле «робот» (на 0:07 движения танцора очень плавные, а на 00:38 он показывает уже стробоскопический эффект).
• Синус меняет свою скорость: начинает двигаться быстро, замедляется, останавливается, а затем снова ускоряется. Ох уж эти очаровательные переходы в танце! (на 0:12 и 0:23 можно увидеть настоящую человеческую синусоиду, а на 00:47 — естественная упругость).

К сожалению, в учебниках танцы не показывают в качестве примера синусоиды. Авторам больше нравится представлять синусоиду изменяющейся во времени (установите «horizontal» в графе «timeline»):

(Википедия)

Проклятие. Вот этот схематический график нам всегда и показывали. Вы по нему представляете, что такое синус? Примерно также, как если бы вас заставили представить ловкость кота по изображению его скелета. Давайте сначала изучим синус в движении, а потом, конечно, изобразим его на графике.

Использование формул

Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.

Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.

Пример 8

Найдите значение tgπ8 . 

Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22 

Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1

tgπ8=2-1.

Рубрика «Вопросы и ответы»

Первый раз, изучая синусы, я упустил несколько вещей:

Синус вообще-то 1-мерный.

Синус движется в одном измерении. Правда. Мы часто рисуем синус, изменяющийся во времени, а иногда и «предмет», описывающий своим движением синус, тоже куда-то движется, но это уже опционально! Скачок в одном направлении — вполне себе полноценная волна синусоиды.

Окружности — это пример синусных волн.

Окружности и квадраты — это комбинации базовых элементов (синусов и прямых отрезков). Но окружности не являются основой синусоиды, как и квадрат не является составной частью прямой.

Что показывают значения синуса?

Синус принимает значения от -1 до 1. Он начинается с 0, возрастает до 1.0 (максимум), падает до -1.0 (минимум) и снова возвращается в нейтральную точку, к нулю. Я также вижу синус как процент от 100% (полный вперёд!) до -100% (полный обратный ход).

Что означает вводное значение ‘x’ в функции sin(x)?

Каверзный вопрос. Поскольку это цикл и х — вводный параметр, он означает, как далеко мы прошли по окружности.

Рассмотрим пример с линиями:

• Мы бродим по квадрату. За 10 секунд мы проходим каждую сторону.
• Спустя 1 секунду, вы прошли 10% от одной стороны
• Спустя 5 секунд, вы прошли одну сторону на 50%
• Через 10 секунд вы пройдете всю сторону.

В линейном движении есть парочка сюрпризов. Рассмотрим теперь синус (сфокусируемся на цикле «от 0 до максимума»):

• Мы путешествуем по синусоиде, стартуя с 0 (нейтральная точка) до 1.0 (максимум). И на этот путь у нас ушло 10 секунд.
• Спустя 5 секунд мы…прошли 70%! Синус очень быстрый на старте, и потихоньку замедляется к вершине. Так что большую часть пути мы пройдем за первые 5 секунд.
• И еще 5 секунд нам потребуется на то, чтобы пройти с 70% до 100% пути. А отрезок с 98% до 100% занимает почти целую секунду!

Несмотря на высокую начальную скорость, синус замедляет свой рост, так что мы очень плавно касаемся точки максимума и разворачиваемся назад. Эта плавность и делает синус синусом.

Если вам очень интересны подробности, нажмите «show stats» в симуляторе. Вы увидите процент выполнения полного цикла, мини-цикла (с 0 до 1.0) и текущее значение. Остановите движение (кнопка Stop), попереключайтесь между линейным и синусоидальным движением, чтобы сравнить значения.

Маленькая проверка: Что будет дальше, 10% линейного цикла или 10% синусного? Правильный ответ — синусного.

Помните, в самом начале синус максимально ускорен. Ко времени достижения 50% цикла, синус движется со средней скоростью линейного цикла и, более того, замедляется (пока не достигнет максимума и не развернется).

Так что x — это «количество вашего цикла». Какого цикла?

Зависит от контекста.

• Базовый вариант: ‘x’ — это градусы, и полный цикл состоит из 360 градусов
• Продвинутый вариант: ‘x’ — это радианы (они более натуральные!) и полный цикл составляет полный проход по единичной окружности (2*π радиан)

Поэкспериментируйте со значением х здесь:

Но опять же, циклы зависят от окружностей! Можем ли мы как-то вырваться из-под их тирании?

Котангенс угла

Помимо тангенса в тригонометрии выделяют ещё одну производную ф-цию – котангенс. Он представляет отношение косинуса к синусу:

Видно, что определение котангенса очень похоже определение тангенса. В принципе, удобней использовать несколько другую формулу:

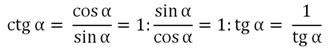
Почти во всех задачах с помощью формулы

можно избавиться от котангенса, заменив его дробью 1/tgα. Поэтому мы вкратце расскажем об основных особенностях котангенса, ведь он очень редко используется на практике.

Значения этой ф-ции рассчитываются так:

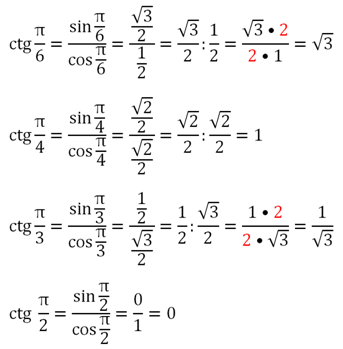
При х = 0 значение котангенса не определено, так как в этой точке косинус становится равным нулю, а деление на ноль невозможно.

График котангенса – это тангенсоида, которая отображена симметрично относительно оси Ох и смещена на π/2:

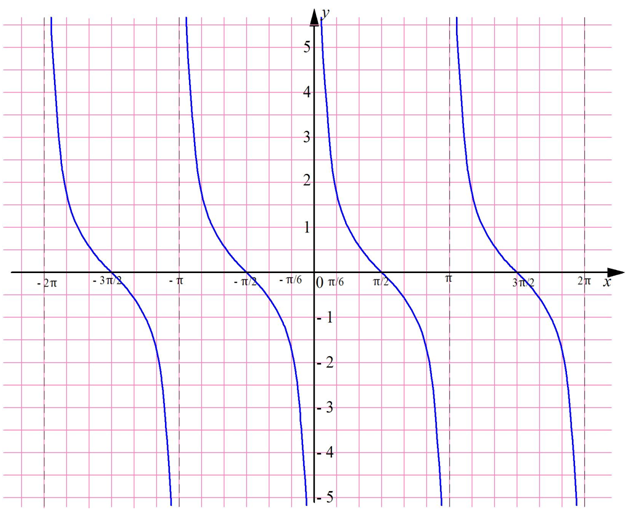
Можно заметить, что вертикальные штриховые линии (асимптоты) графика проходят через точки, кратные π: –2π, – π, 0, π, 2π… Они разбивают координатную прямую на интервалы (– 2π; – π), (– π; 0), (0; π), (π; 2π), на каждом из которых ф-ция у = ctgx убывает. Видно, что котангенс – это периодическая ф-ция с периодом π.

Для сравнения покажем на одной плоскости графики тангенса и котангенса:

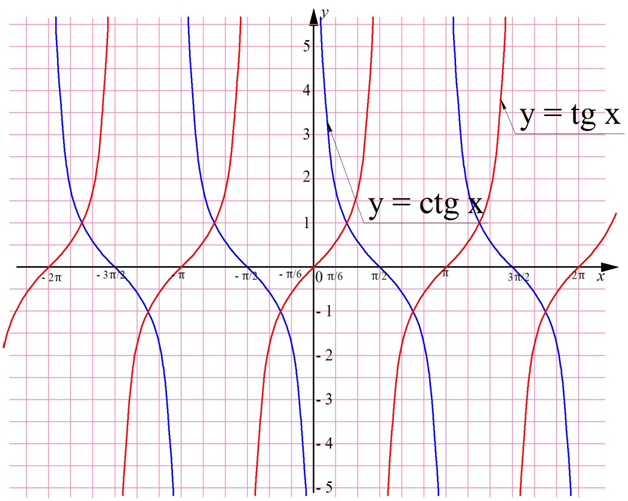
Котангенс, как и тангенс – нечетная ф-ция, то есть

ctg (– x) = – ctgx

Теперь у нас есть представление об основных тригонометрических ф-циях. Важнейшими из них являются синус и косинус. Тангенс является производной ф-цией от них и рассчитывается как отношение синуса к косинусу. Редко используемый котангенс, наоборот, представляет собой отношение косинуса к синусу.

Впервые элементы тригонометрии стали использовать ещё древние греки, которые производили с их помощью астрономические расчеты. В XVIII веке Эйлер сформулировал определения тригонометрических функций с помощью единичной окружности, благодаря которым стало возможным вычислять их значение для любых углов. Изначально тригонометрия использовалась для географических расчетов и навигации, однако со временем область ее применения расширилась. Оказалось, что без неё не обойтись в анализе финансовых рынков и биологических процессов, архитектуре, акустике и оптике, теории вероятностей.

Прямоугольный треугольник

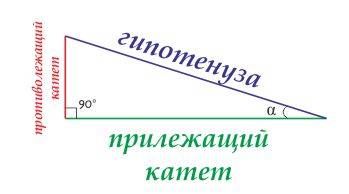
гипотенуза – сторона прямоугольного треугольника, лежащая против прямого угла и являющаяся самой длинной стороной прямоугольного треугольника.

катет – одна из сторон прямоугольного треугольника, образующая прямой угол треугольника. Может называться противолежащим или прилежащим. Противолежащий – это катет, расположенный напротив рассматриваемого угла треугольника, прилежащий – это катет, прилежащий к рассматриваемому углу треугольника.

Чтобы вычислить какой-либо неизвестный элемент (сторону или угол) имеющегося треугольника, зная часть элементов того же треугольника, используют определенные зависимости (правила) между величинами углов и длинами сторон этого треугольника. Такие зависимости называют тригонометрическими функциями.

К базовым тригонометрическим функциям относятся:

То есть, тригонометрические функций позволяют, зная какой-либо угол и сторону, вычислить значения других неизвестных элементов треугольника.

Графики функций с модулем

Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.

Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.

Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.

Правило: график функции  получается из графика функции  следующим образом: при  график функции  сохраняется, а при  «сохранённая часть» отображается симметрично относительно оси .

Пример 22

Построить график функции

И снова вечная картина:
Согласно правилу, при  график сохраняется:
И сохранившаяся часть отображается симметрично относительно оси   в левую полуплоскость:

Действительно, функция  – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на  и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.

Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае:

То есть, правая волна графика  задаётся функцией , а левая волна – функцией  (см. Пример 13).

Пример 23

Построить график функции

Аналогично, ветвь «обычной» экспоненты  правой полуплоскости отображаем симметрично относительно оси  в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .

Модуль не имеет смысл «навешивать» на аргумент чётной функции:  и т.п. (проанализируйте, почему).

И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.

Правило: график функции  получается из графика функции  следующим образом: часть графика , лежащая НАД осью  сохраняется, а часть графика , лежащая ПОД осью  отображается симметрично относительно данной оси.

Странно, что широко известный график модуля «икс» оказался на 24-й позиции, но факт остаётся фактом =)

Пример 24

Построить график функции

Сначала начертим прямую, известную широкому кругу лиц:
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси  – отображается симметрично в верхнюю полуплоскость:

Модуль функции также раскрывается аналитически в кусочном виде:

Внимание! Формула отличается от формулы предыдущего пункта!

В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .

Кстати,  – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и  к самой функции: . Изучим более «жизненную» ситуацию:

Пример 25

Построить график функции

Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси  в верхнюю полуплоскость:

Согласно формуле , распишем функцию аналитически в кусочном виде: .

Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.

На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .

Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:

Пример 26

Построить график функции .

Изобразим сами знаете что =)

И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :

Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у  отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.

Распишем функцию в кусочном виде:

Решив два простейших школьных неравенства , получаем:, где  – любое целое число.

Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)

Желаю успехов!

(Переход на главную страницу)

Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?

Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A(1, ) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно. 

Для наглядности приведем иллюстрацию.

                                     

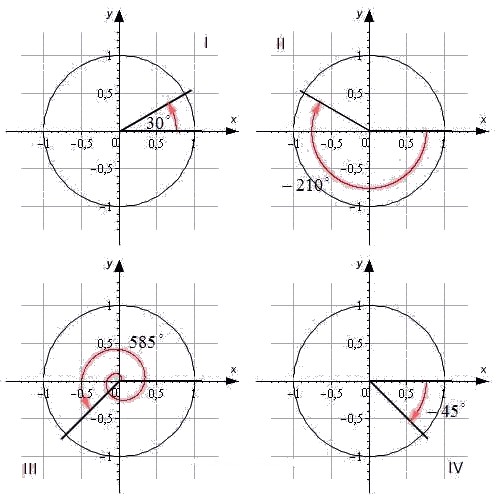
Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° — угол третьей четверти. Угол -45° —  это угол четвертой четверти.

При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.

Косинус — это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

                                  

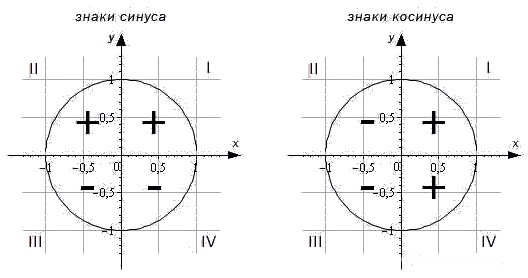
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям. 

                                 

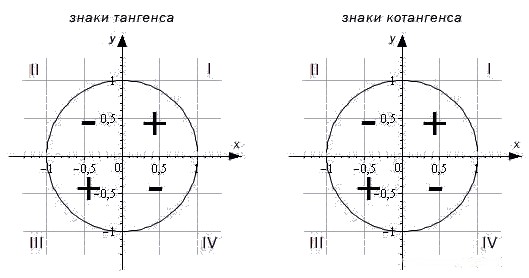
Важно помнить!

1. Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
2. Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
3. Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
4. Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.

Определение 3: Дифференциальное уравнение

Мы описали поведение синуса определенными уравнениями. Вкратце это будет выглядеть так:

Эта красота означает следующее:

Наша текущая позиция — y

Наше ускорение (2-я производная, или у”) — обратно нашей текущей позиции (-y)

Это справедливо и для синуса, и для косинуса. Сначала я просто ненавидел это определение; оно такое непохожее на нашу визуализацию. Я не понимал, что оно описывало суть синуса: «ускорение, обратное текущей позиции».

И вспомните как синус и е связаны? Ну, e^x можно описать уравнением:

То же уравнение с положительным знаком («ускорение равно текущей позиции»)! Когда синус — это «высота окружности», очень тяжело проследить связь с е.

Одним из моих серьезнейших математических сожалений является то, что я еще не изучил дифференциальные уравнения. Но я хочу это сделать, и подозреваю, что правильное понимание синуса и экспоненты сыграют в этом решающую роль.